190. 颠倒二进制位

题目：

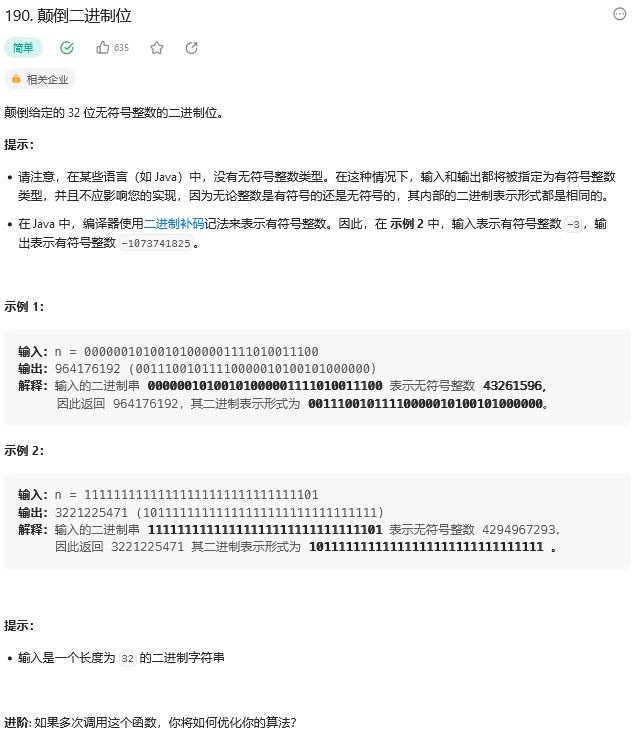
思路：

【1】重点是位理念和溢出的问题

代码展示：

//时间2 ms 击败 3.44%
//内存39.8 MB 击败 77.56%
public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        // 这里采用byte数组是为了减少用到的内存
        byte[] bit = new byte[32];
        char[] ch = Integer.toBinaryString(n).toCharArray();
        int dif = bit.length - ch.length;
        for (int i = 0; i < 16; i++){
            bit[i] = (byte) (ch.length - 1 - i >= 0 ? ch[ch.length - 1 - i] - '0' : 0);
            bit[bit.length - 1 - i] = (byte) (i < (dif) ? 0 : ch[i - dif] - '0');
        }
        //然后转为字符串再生成无符号的int
        StringBuffer buf = new StringBuffer();
        for (int i = 0; i <bit.length ;i++){
            buf.append(bit[i]);
        }
        return Integer.parseUnsignedInt(buf.toString(),2);
    }
}

//时间1 ms 击败 9.83%
//内存39.6 MB 击败 93.53%
//使用累加的方式
public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        // 这里采用byte数组是为了减少用到的内存
        byte[] bit = new byte[32];
        char[] ch = Integer.toBinaryString(n).toCharArray();
        int dif = bit.length - ch.length;
        for (int i = 0; i < 16; i++){
            bit[i] = (byte) (ch.length - 1 - i >= 0 ? ch[ch.length - 1 - i] - '0' : 0);
            bit[bit.length - 1 - i] = (byte) (i < (dif) ? 0 : ch[i - dif] - '0');
        }
        //然后累加得到结果
        //这里是要特殊处理的因为Math.pow(2,(bit.length-1-i)) 本质上应该是2147483648
        //但是转为int的时候由于溢出问题会被转为 2147483647，这样就会少了1，故要特殊处理
        int res = bit[0] == 1 ? Integer.MAX_VALUE + 1 : 0;
        for (int i = 1; i <bit.length ;i++){
            res += (int) (bit[i]*Math.pow(2,(bit.length-1-i)));
        }
        // 使用累加的方式是得不到正确的结果的（所以直接拿到对应的二进制字符串生成无符号int数据）
        // 因为一旦出现负数的时候如 -7 + 5 = -2 ，本质上是倒退了 
        return res;
    }
}

//时间1 ms 击败 9.83%
//内存39.6 MB 击败 93.24%
public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        int rev = 0;
        for (int i = 0; i < 32 && n != 0; ++i) {
            rev |= (n & 1) << (31 - i);
            n >>>= 1;
        }
        return rev;
    }
}

//时间0 ms 击败 100%
//内存39.7 MB 击败 84.40%
public class Solution {
    // you need treat n as an unsigned value
    private static final int M1 = 0x55555555; // 01010101010101010101010101010101
    private static final int M2 = 0x33333333; // 00110011001100110011001100110011
    private static final int M4 = 0x0f0f0f0f; // 00001111000011110000111100001111
    private static final int M8 = 0x00ff00ff; // 00000000111111110000000011111111

    public int reverseBits(int n) {
        n = n >>> 1 & M1 | (n & M1) << 1;
        n = n >>> 2 & M2 | (n & M2) << 2;
        n = n >>> 4 & M4 | (n & M4) << 4;
        n = n >>> 8 & M8 | (n & M8) << 8;
        return n >>> 16 | n << 16;
    }
}