274. H 指数（275. H 指数 II）

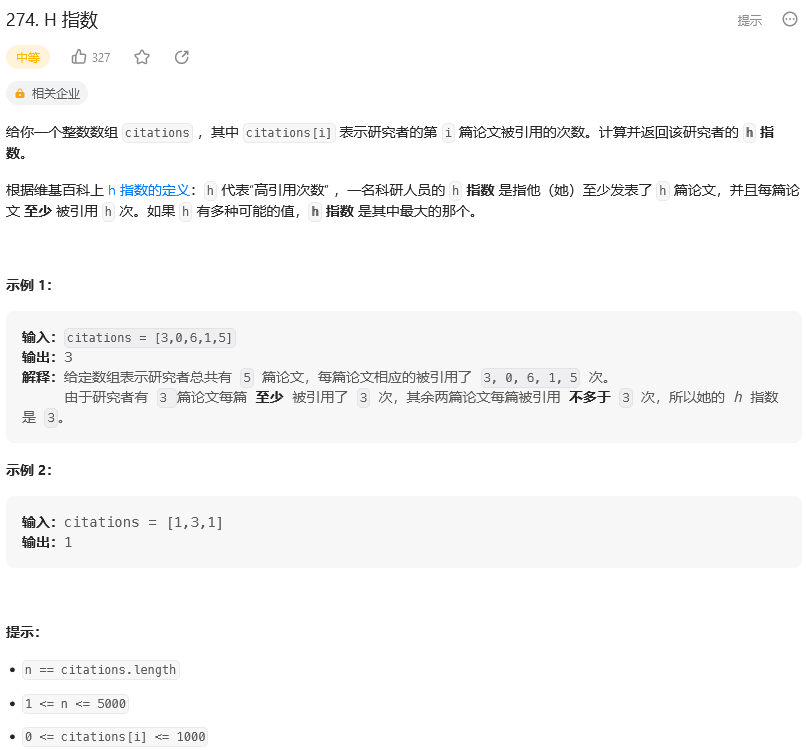
题目：

思路：

【1】274. H 指数

【1.1】明确题目

该题目，主要是理解题意即可
条件：需要同时满足文章数>=h，且每篇文章的引用数>=h
如[3,0,6,1,5] 排序后为 [0,1,3,5,6]

可以发现引用数大于等于1的有4篇
可以发现引用数大于等于3的有3篇
可以发现引用数大于等于5的有2篇
可以发现引用数大于等于6的有1篇
由于需要的是满足条件，故选三最为合适

【2】275. H 指数 II

代码展示：

【2】275. H 指数 II

//时间0 ms 击败 100%
//内存49.4 MB 击败 49.38%
class Solution {
    public int hIndex(int[] citations) {
        int l = 0, r = citations.length , n = citations.length;
        while (l < r) {
            int mid = (l + r) >> 1;
            int x = mid < n ? citations[mid] : Integer.MAX_VALUE;
            // 核心在于这个判断 如果当前中位数值是合法的
            // 那么它引用的次数必定要大于或者等于当前位置到右边界的全部篇幅
            if (x >= n - mid) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        // 找到最左边的第一个合法引用文章那么计算出它到右边界的篇幅即可
        return n - l;
    }
}

【1】274. H 指数

//时间1 ms 击败 85.57%
//内存39.1 MB 击败 94.81%
//时间复杂度：O(nlog⁡n)，其中 n 为数组 citations的长度。即为排序的时间复杂度。
//空间复杂度：O(log⁡n)，其中 n 为数组 citations。即为排序的空间复杂度。
class Solution {
    public int hIndex(int[] citations) {
        //按升序排序（越大的排在越后面）
        Arrays.sort(citations);
        int h = 0, i = citations.length - 1;
        //判断引用数和文章数都大于h
        while (i >= 0 && citations[i] > h) {
            h++;
            i--;
        }
        return h;
    }
}


//时间0 ms 击败 100%
//内存39.2 MB 击败 89.76%
//时间复杂度：O(n)，其中 n 为数组 citations 的长度。
//需要遍历数组 citations 一次，以及遍历长度为 n+1 的数组 counter 一次。
//空间复杂度：O(n)，其中 n 为数组 citations 的长度。
//需要创建长度为 n+1 的数组 counter。
class Solution {
    public int hIndex(int[] citations) {
        int n = citations.length, tot = 0;
        int[] counter = new int[n + 1];
        for (int i = 0; i < n; i++) {
            if (citations[i] >= n) {
                counter[n]++;
            } else {
                counter[citations[i]]++;
            }
        }
        for (int i = n; i >= 0; i--) {
            tot += counter[i];
            if (tot >= i) {
                return i;
            }
        }
        return 0;
    }
}