189. 轮转数组

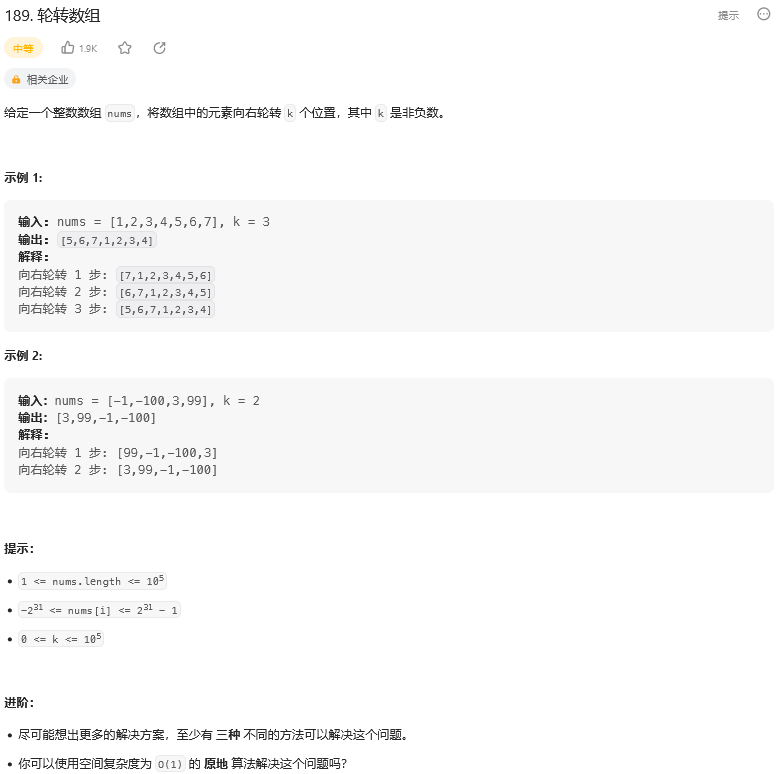
题目：

思路：

【1】如果采用辅助空间（这种是最简单的，因为需要遍历一遍，然后放入指定位置）

【2】对于进阶的处理，即只用空间复杂度为O(1)

【2.1】利用环的思维

其实这里需要理解一个比较绕的逻辑
就是从X位置开始循环，到回到X位置到底遍历了多少个元素
已知数组的元素个数是n，偏移量为k
（这个k < n,如果k>n,则k = k%n，因为n=7，而k=9的话其实不会是绕了一圈再偏移2而已，所以不如一开始就偏移2）

由于最终回到了起点，故该过程恰好走了整数数量的圈，不妨设为 a 圈；再设该过程总共遍历了 b 个元素。
因此，我们有 an=bk，即 an 一定为 n,k 的公倍数（且是最小公倍数）。
又因为我们在第一次回到起点时就结束，因此 aaa 要尽可能小，
故 an 就是 n,k 的最小公倍数 lcm(n,k)，
因此 b 就为 lcm(n,k)/k。
即假设n=7，k=3，你就会发现圈数刚好是3，而遍历的个数恰好也是7。
为什么是最小公倍数呢，你往大了增，就是21的两倍三倍都没什么意义，不过是多饶了几圈
而既然有了b那么 n/b 就是表示应该要有几个数循环
如n=6，k=2，就要循环0和1
而n=7，k=3，只需要循环0
即 n/b = n*k/lcm(n,k) = 最大公约数 gcd(n,k)

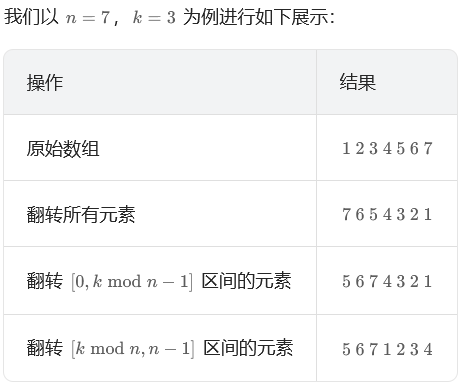
【2.2】数组的翻转

代码展示：

采用辅助空间：

//时间1 ms 击败 62.57%
//内存54.2 MB 击败 77.43%
//时间复杂度： O(n)，其中 n 为数组的长度。
//空间复杂度： O(n)。
class Solution {
    public void rotate(int[] nums, int k) {
        int count = nums.length;
        // 这里之所以这样处理是因为K可能大于nums.length，
        // 如果K=9，而nums.length = 7，那么不过是转了一圈后再偏移2
        int drift = k % count;
        //生成要借助的辅助空间且拷贝数据
        int[] result = Arrays.copyOf(nums,count);

        int i = 0;
        //先将数据从前部分偏移固定位置向后放置
        for (; i < count - drift; i++){
            nums[i + drift] = result[i];
        }
        //然后将需要前置的数据放入前置的位置
        int index = 0;
        for (; i < count; i++){
            nums[index++] = result[i];
        }
    }
}

//时间1 ms 击败 62.57%
//内存54.1 MB 击败 89.25%
class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        int[] newArr = new int[n];
        for (int i = 0; i < n; ++i) {
            newArr[(i + k) % n] = nums[i];
        }
        System.arraycopy(newArr, 0, nums, 0, n);
    }
}

 

 

 

利用环的思维：

//时间1 ms 击败 62.57%
//内存54.1 MB 击败 85.81%
class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k = k % n;
        //重点在于这个最大公约数
        int count = gcd(k, n);
        for (int start = 0; start < count; ++start) {
            int current = start;
            int prev = nums[start];
            do {
                int next = (current + k) % n;
                int temp = nums[next];
                nums[next] = prev;
                prev = temp;
                current = next;
            } while (start != current);
        }
    }

    /**
     * 根据用欧几里得算法获取最大公约数
     * 如需要求 1255 和 840 两个正整数的最大公约数，是这样进行的：
     * 1255 ÷ 840 余 415
     * 840 ÷ 415 余 10
     * 415 ÷ 10 余 5
     * 10 ÷ 5 余 0
     * 至此，最大公约数为5
     * @return 最大公约数
     */
    public int gcd(int x, int y) {
        return y > 0 ? gcd(y, x % y) : x;
    }
}

 

 

 

数组的翻转：

//时间0 ms 击败 100%
//内存54.2 MB 击败 82.93%
//时间复杂度：O(n)，其中 n 为数组的长度。
//每个元素被翻转两次，一共 n 个元素，因此总时间复杂度为 O(2n)=O(n)。
//空间复杂度：O(1)。
class Solution {
    public void rotate(int[] nums, int k) {
        int n=nums.length;
        k=k%n;
        reverse(nums,0,n-1);
        reverse(nums,0,k-1);
        reverse(nums,k,n-1);
    }

    private void reverse(int[] nums,int start,int end){
        while (start<end){
            int tmp=nums[start];
            nums[start]=nums[end];
            nums[end]=tmp;
            start++;
            end--;
        }
    }
}