42. 接雨水

题目：

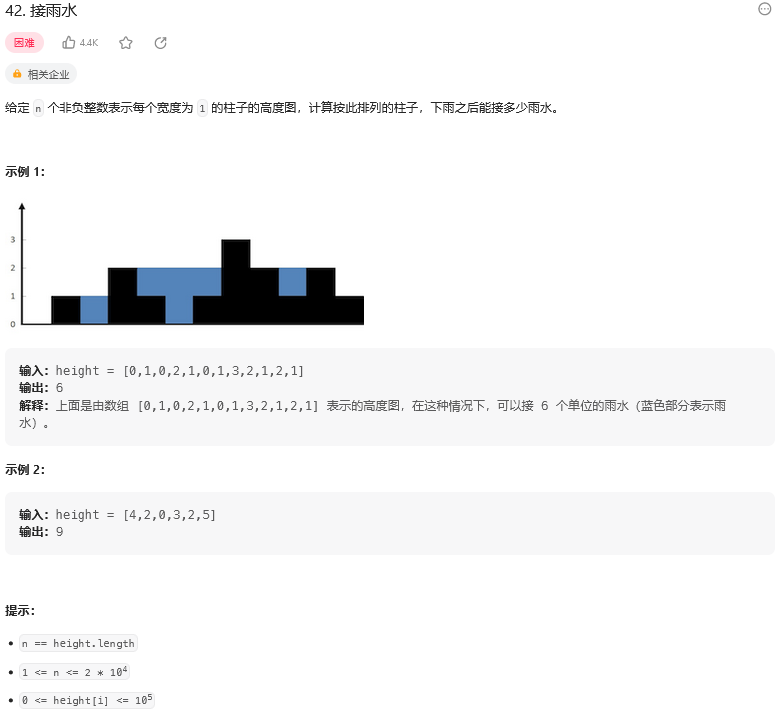
思路：

【1】双指针的做法（这题类似于 11. 盛最多水的容器）：

【2】动态规划（可以理解为双指针的基础版）

如图：

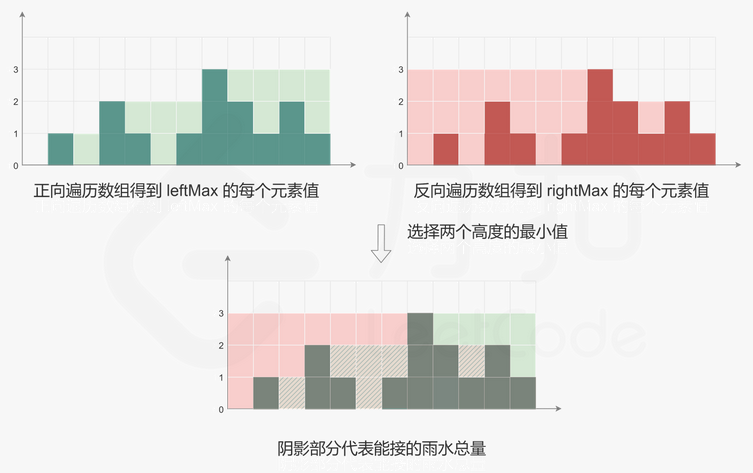
【3】

代码展示：

双指针的做法：

//时间0 ms 击败 100%
//内存43.7 MB 击败 6.18%
//时间复杂度：O(n)，其中 n 是数组 height 的长度。
//两个指针的移动总次数不超过 n。
//空间复杂度：O(1)。只需要使用常数的额外空间。
class Solution {
    public int trap(int[] height) {
        int ans = 0;
        int left = 0, right = height.length - 1;
        int leftMax = 0, rightMax = 0;
        while (left < right) {
            //获取两边的最大边界
            leftMax = Math.max(leftMax, height[left]);
            rightMax = Math.max(rightMax, height[right]);
            //这里是确保低的一方先计算，而且是那边低那边就会先移动，确保最高边作为边界
            if (height[left] < height[right]) {
                ans += leftMax - height[left];
                ++left;
            } else {
                ans += rightMax - height[right];
                --right;
            }
        }
        return ans;
    }
}

动态规划的方式：

//时间1 ms 击败 79.10%
//内存43.3 MB 击败 22.57%
//时间复杂度：O(n)，其中 n 是数组 height 的长度。
//计算数组 leftMax 和 rightMax 的元素值各需要遍历数组 height 一次，计算能接的雨水总量还需要遍历一次。
//所以算是由O(3n)变为的O(n).
//空间复杂度：O(n)，其中 n 是数组 height 的长度。
//因需要创建两个长度为 n 的数组 leftMax 和 rightMax，故是由O(2n)变为的O(n)
class Solution {
    public int trap(int[] height) {
        int n = height.length;
        if (n == 0) {
            return 0;
        }

        int[] leftMax = new int[n];
        leftMax[0] = height[0];
        for (int i = 1; i < n; ++i) {
            leftMax[i] = Math.max(leftMax[i - 1], height[i]);
        }

        int[] rightMax = new int[n];
        rightMax[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; --i) {
            rightMax[i] = Math.max(rightMax[i + 1], height[i]);
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans += Math.min(leftMax[i], rightMax[i]) - height[i];
        }
        return ans;
    }
}