剑指 Offer II 079. 所有子集（78. 子集）

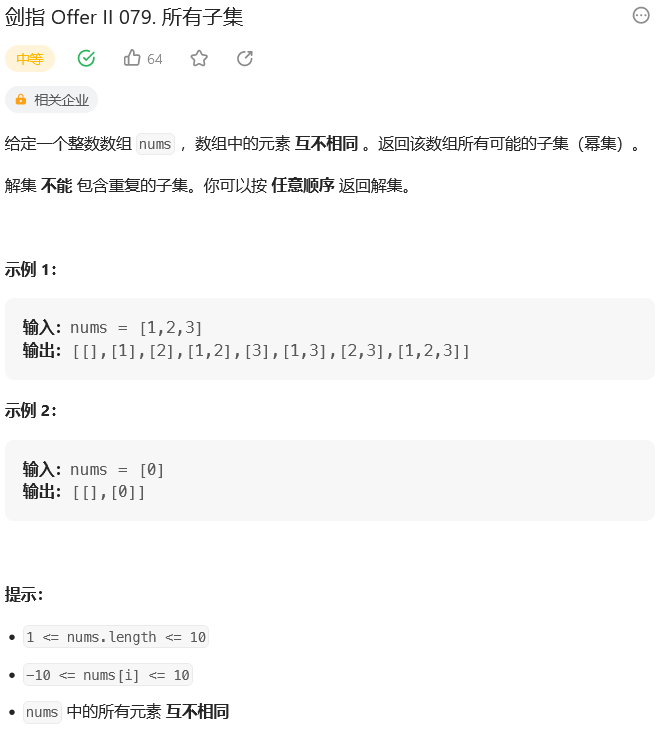
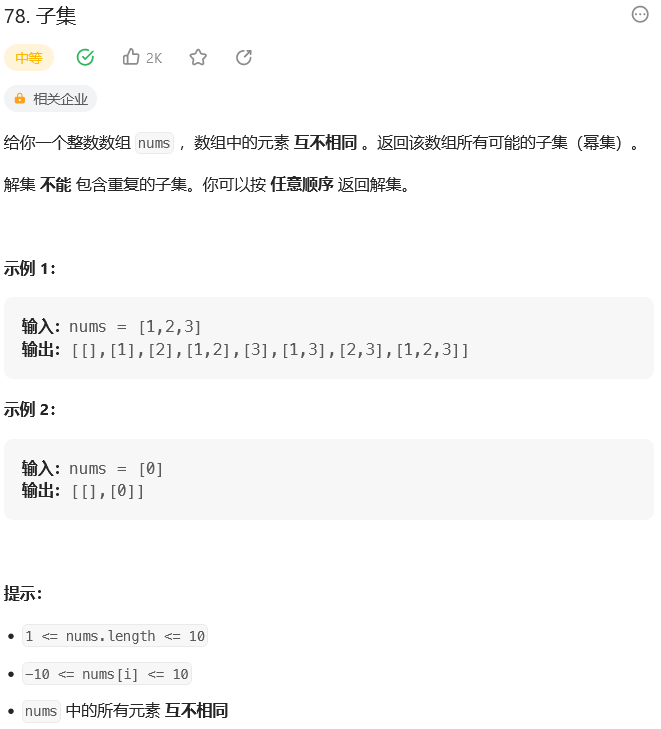
题目：

思路：

【1】利用二进制特性，双循环迭代

【2】利用树特性，进行检索

代码展示：

【1】利用二进制特性，双循环迭代：

//时间1 ms击败29.10%
//内存40.7 MB击败98.77%
//时间复杂度：O(n×2^n)。一共 2^n 个状态，每种状态需要 O(n) 的时间来构造子集。
//空间复杂度：O(n)。即构造子集使用的临时数组 t 的空间代价。
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<Integer> t = new ArrayList<Integer>();
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        int n = nums.length;
        //子集在于选择集合里面的元素，而选法如二进制展示
        //采用了int数字替代用来展示为二进制，如
        //0  = 二进制000
        //1  = 二进制001
        //2  = 二进制010
        //3  = 二进制011 ...
        for (int mask = 0; mask < (1 << n); ++mask) {
            t.clear();
            for (int i = 0; i < n; ++i) {
                //表示该位置是被选择的
                if ((mask & (1 << i)) != 0) {
                    t.add(nums[i]);
                }
            }
            ans.add(new ArrayList<Integer>(t));
        }
        return ans;
    }
}

 

【2】利用树特性，进行检索：

//时间0 ms击败100%
//内存40.7 MB击败98.69%
//时间复杂度：O(n×2^n)。一共 2^n 个状态，每种状态需要 O(n) 的时间来构造子集。
//空间复杂度：O(n)。临时数组 t 的空间代价是 O(n)，递归时栈空间的代价为 O(n);
class Solution {
    List<Integer> t = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ans;
    }

    public void dfs(int cur, int[] nums) {
        if (cur == nums.length) {
            ans.add(new ArrayList<Integer>(t));
            return;
        }
        t.add(nums[cur]);
        dfs(cur + 1, nums);
        t.remove(t.size() - 1);
        dfs(cur + 1, nums);
    }
}