剑指 Offer II 039. 直方图最大矩形面积（84. 柱状图中最大的矩形）

题目：

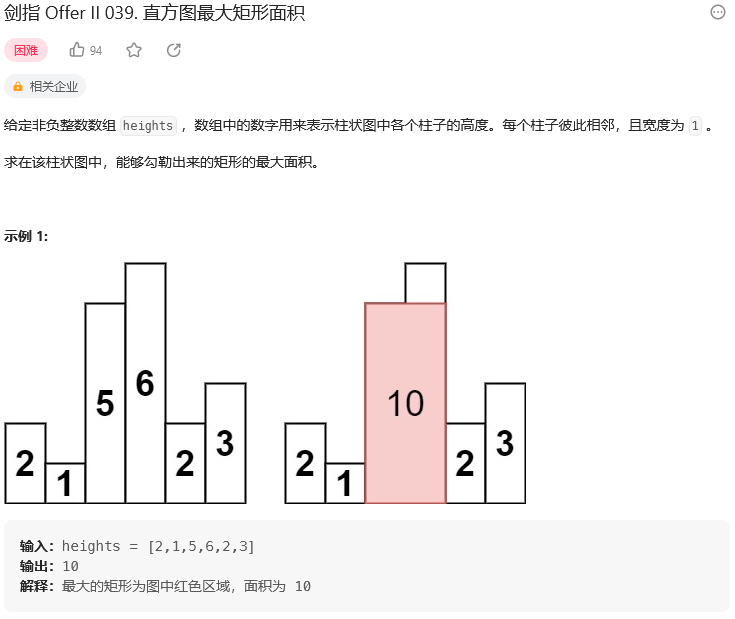
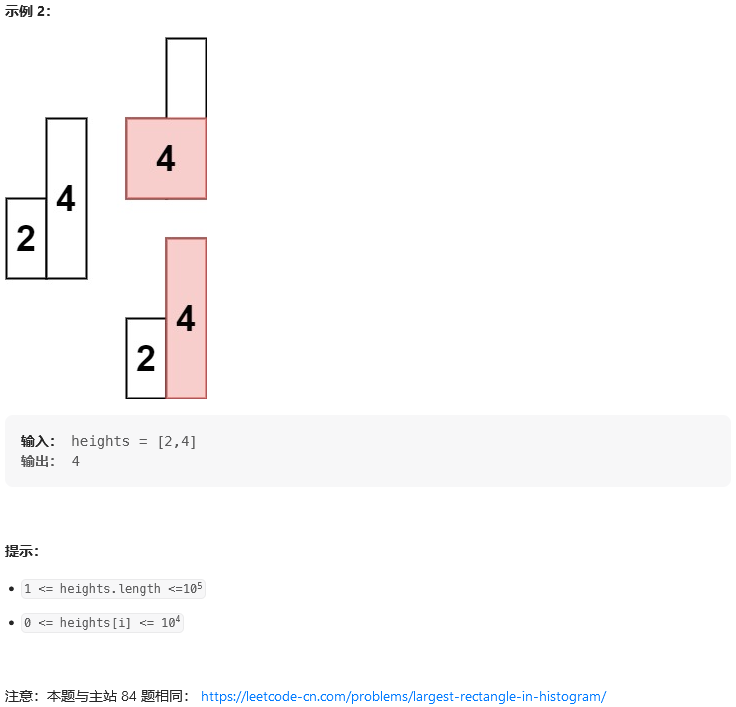
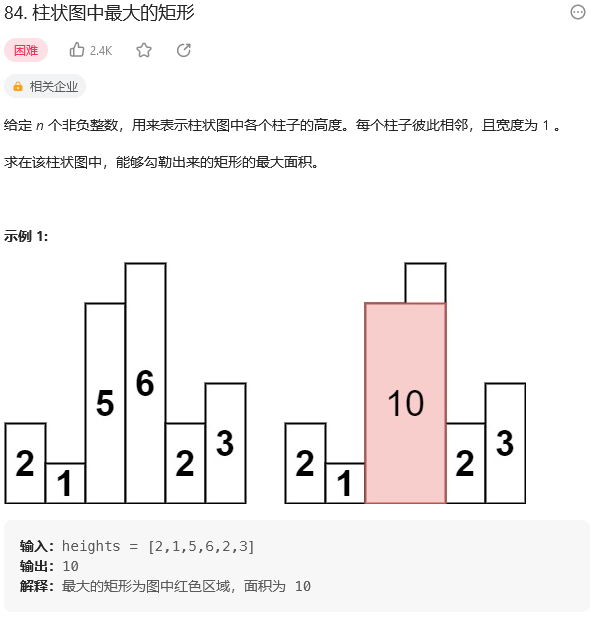
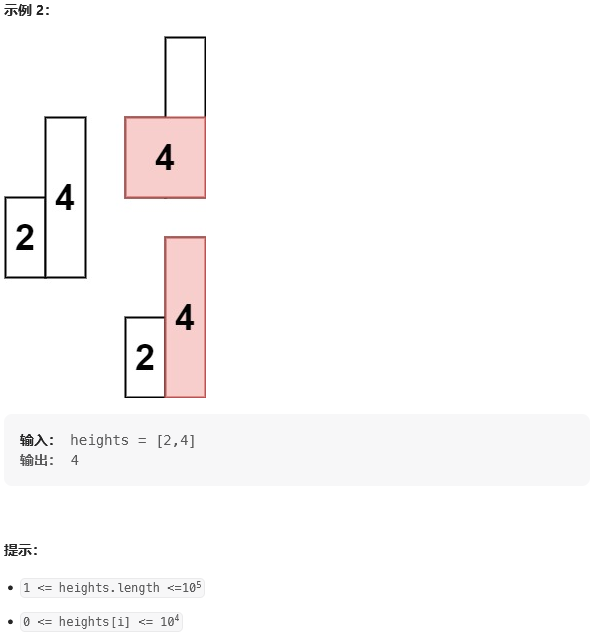
思路：

【1】以中心扩散为思路的暴力破解方法

 

 

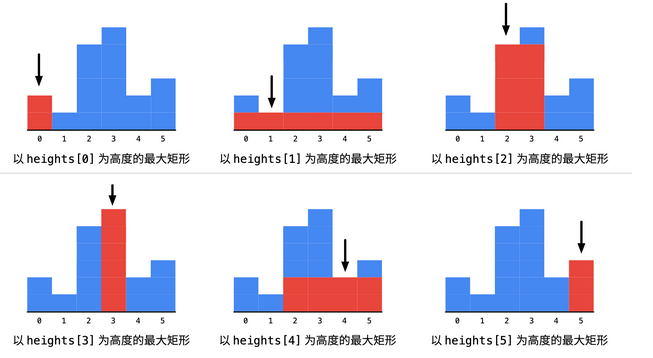
【2】单调栈的方式（基础模型：在一维数组中对每一个数找到第一个比自己小的元素。这类“在一维数组中找第一个满足某种条件的数”的场景就是典型的单调栈应用场景。）【其实可以参考  剑指 Offer 30. 包含min函数的栈  】

代码展示：

单调栈 + 常数优化：

//时间18 ms击败81.16%
//内存50 MB击败91.3%
class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(right, n);
        
        Deque<Integer> mono_stack = new ArrayDeque<Integer>();
        for (int i = 0; i < n; ++i) {
            while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
                right[mono_stack.peek()] = i;
                mono_stack.pop();
            }
            left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
            mono_stack.push(i);
        }
        
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
}

 

 

 

单调栈的方式：

//时间24 ms击败52.4%
//内存55.7 MB击败29.11%
//时间复杂度：O(N)。
//空间复杂度：O(N)。
class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] left = new int[n];
        int[] right = new int[n];
        //以{2,1,5,6,2,3}为例
        Deque<Integer> mono_stack = new ArrayDeque<Integer>();
        for (int i = 0; i < n; ++i) {
            //如果不为空则存在下标，下标位置的值如果比当前值要大则弹出，因为只会保留距离当前值最近的左边的最小值
            while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
                mono_stack.pop();
            }
            //如果不为空则发现附近的最小值，没有则会延伸至边界
            left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
            //这里是记录下标
            mono_stack.push(i);
        }
        System.out.println(Arrays.toString(left));

        mono_stack.clear();
        for (int i = n - 1; i >= 0; --i) {
            while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
                mono_stack.pop();
            }
            right[i] = (mono_stack.isEmpty() ? n : mono_stack.peek());
            mono_stack.push(i);
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
}

 

 

 

以中心扩散为思路进行的优化：

//时间6 ms击败96.90%
//内存54.8 MB击败40.61%
class Solution {
    public int largestRectangleArea(int[] heights) {
        int max = 0;
        int left = 0;
        int right = 0;
        for(int i =0;i<heights.length;i++){
            left = i-1;
            right = i+1;
            //这里可以减少当数据量过大时候不必要的扩散
            //首先如果你扩散到了极致（即整个数组的长度），配合你的高度都比不过我现在的最大值，那么你就没有扩散的必要了
            if(heights.length * heights[i]>max){
                while(left>=0 && heights[left]>=heights[i]){
                    left--;
                }
                while(right<=heights.length-1 && heights[right]>=heights[i]){
                    right++;
                }
                max = Math.max(max,(right - left - 1)*heights[i]);
            }
        }
        return max;
    }
}

 

以中心扩散为思路的暴力破解方法：

//在运行的时候是会出现超时的
//时间复杂度：O(N^2)，这里 N 是输入数组的长度。
//空间复杂度：O(1)。
//因为本身就是基于每一个点都会向两边扩散，直至找到最大的矩阵范围（而且高度是基于当前位置的高度）
class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;

        int res = 0;
        for (int i = 0; i < len; i++) {

            // 找左边最后 1 个大于等于 heights[i] 的下标
            int left = i;
            int curHeight = heights[i];
            while (left > 0 && heights[left - 1] >= curHeight) {
                left--;
            }

            // 找右边最后 1 个大于等于 heights[i] 的索引
            int right = i;
            while (right < len - 1 && heights[right + 1] >= curHeight) {
                right++;
            }

            int width = right - left + 1;
            res = Math.max(res, width * curHeight);
        }
        return res;
    }
}