剑指 Offer II 115. 重建序列（444. 序列重建）

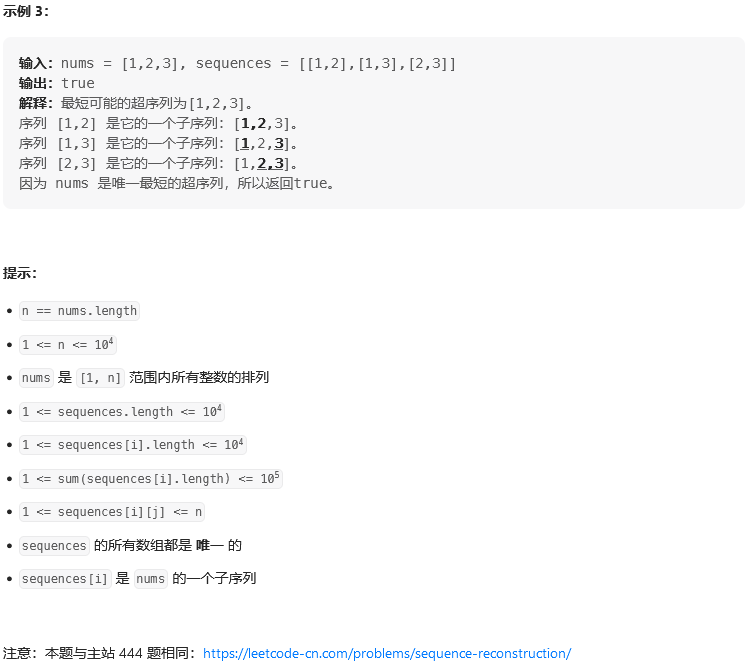
题目：

思路：

【0】首先是读题，看的是玄里玄乎的，但其实本质上就是问sequences是否存在路径能够走完整个nums数组。如nums是【1,2,3】而sequences存在【1,2】和【2,3】，故从1走到2，再从2走到3，实际上便是走完了整个nums数组。

【1】使用边hash比对的方式：

【2】拓扑排序的方式：

代码展示：

拓扑排序的方式：

//时间22 ms击败70.26%
//内存48.8 MB击败62.7%
class Solution {
    public boolean sequenceReconstruction(int[] nums, int[][] sequences) {
        int n = nums.length;
        int[] indegrees = new int[n + 1];
        Set<Integer>[] graph = new Set[n + 1];
        //构建图的结构
        for (int i = 1; i <= n; i++) {
            graph[i] = new HashSet<Integer>();
        }
        //填充图数据，且记录节点的入度数
        for (int[] sequence : sequences) {
            int size = sequence.length;
            for (int i = 1; i < size; i++) {
                int prev = sequence[i - 1], next = sequence[i];
                if (graph[prev].add(next)) {
                    indegrees[next]++;
                }
            }
        }
        Queue<Integer> queue = new ArrayDeque<Integer>();
        //将所有的入度数为0的节点取出
        for (int i = 1; i <= n; i++) {
            if (indegrees[i] == 0) {
                queue.offer(i);
            }
        }
        while (!queue.isEmpty()) {
            // 依据题意有解的话，必然存在一个整条链路，所以入度数为0的只有1，
            // 如果存在其他的必然某一条边是不被纳入的，如【1,2,3,4】，
            // 即只有出现【1,2】，【2,4】，【3,4】这种，1和3入度为0。你要知道如果存在【x,3】那么3的入度必不为0.
            if (queue.size() > 1) {
                return false;
            }
            int num = queue.poll();
            Set<Integer> set = graph[num];
            for (int next : set) {
                indegrees[next]--;
                if (indegrees[next] == 0) {
                    queue.offer(next);
                }
            }
        }
        return true;
    }
}

 

使用边hash比对的方式：

//时间1 ms击败100%
//内存44.1 MB击败90.30%   
// 根据nums中的边构建map，判断nums中的边是否都在sequences中出现
class Solution {
    public boolean sequenceReconstruction(int[] nums, int[][] sequences) {
        int n = nums.length;
        int[] map = new int[n+1];
        int count = 0;
        //由于是要找出nums数组的全部边，那么将其存储下来
        for(int i=0;i<n-1;i++){
            map[nums[i]] = nums[i+1];
            count++;
        }
        //通过遍历sequences，判断是否map中的所有边都是存在的
        for(int[] sequence:sequences){
            for(int i=0;i<sequence.length-1;i++){
                if(map[sequence[i]]==sequence[i+1]){
                    count--;
                    //已经消耗过的边，直接变为-1（这是基于题意，数字在1-n，故变为负数表示消耗），不会重复消耗
                    map[sequence[i]]=-1;
                }
            }
        }
        return count==0;
    }
}