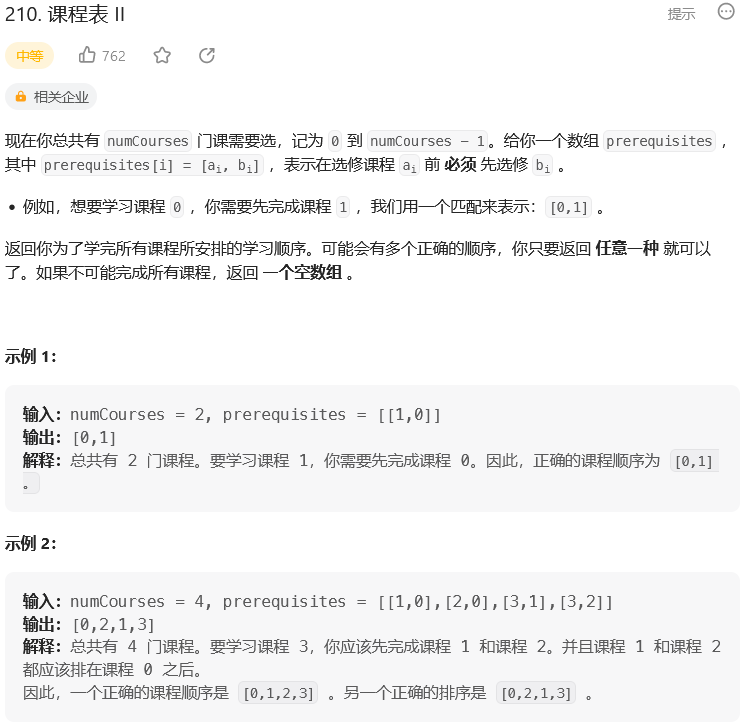
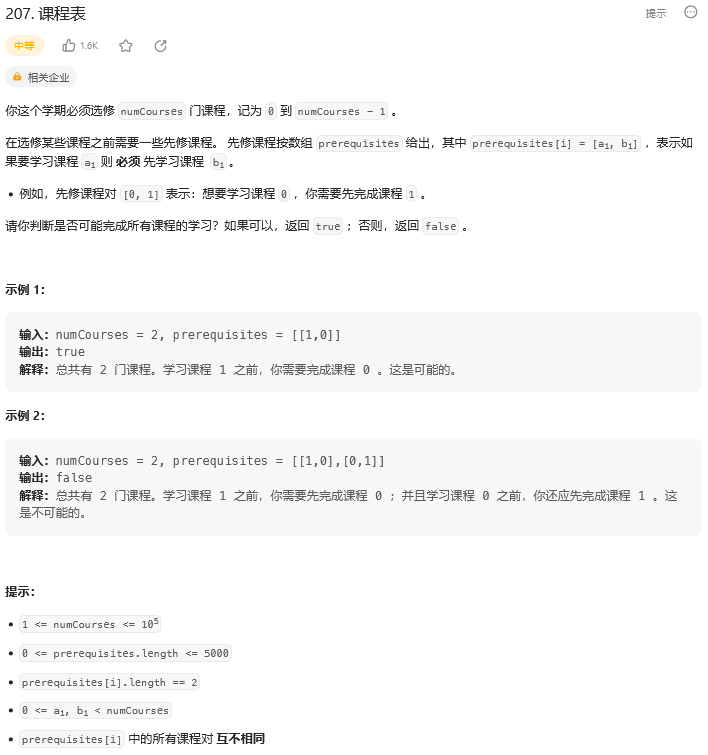
剑指 Offer II 113. 课程顺序(210. 课程表 II && 207. 课程表)
题目:



思路:
【1】广度优先搜索的方式
代码展示:
广度优先搜索的方式:
//时间4 ms击败77.47% //内存42.5 MB击败61.26% //时间复杂度: O(n+m),其中 n 为课程数,m 为先修课程的要求数。 //这其实就是对图进行广度优先搜索的时间复杂度。 //空间复杂度: O(n+m)。 //题目中是以列表形式给出的先修课程关系,为了对图进行广度优先搜索,我们需要存储成邻接表的形式,空间复杂度为 O(n+m)。 //在广度优先搜索的过程中,我们需要最多 O(n) 的队列空间(迭代)进行广度优先搜索, //并且还需要若干个 O(n) 的空间存储节点入度、最终答案等。 //这题的思路本质上是求是否有顺序可以正解 //那么先将入度为0的先放(因为这种不依赖其他的,反而可能是其他课程的依赖), //放入后,其实这个点可以走到的点的入度都应该减1,毕竟都被抽走了(这里可以画图理解一下) //然后依次把全部入度数都为0的塞完后,如果个数不对,即没有解 //因为环是会导致无解的,但由于环的入度不为0,而上面的操作也不可能导致环的点的入度变为0 class Solution { // 存储有向图 List<List<Integer>> edges; // 存储每个节点的入度 int[] indeg; // 存储答案 int[] result; // 答案下标 int index; public int[] findOrder(int numCourses, int[][] prerequisites) { edges = new ArrayList<List<Integer>>(); //构建有向图,如0->[1,2],表示0可以走向1或者2 for (int i = 0; i < numCourses; ++i) { edges.add(new ArrayList<Integer>()); } indeg = new int[numCourses]; result = new int[numCourses]; index = 0; //添加有向图的走向,且记录点的入度情况,即可以由多少个点达到某点 //如1->2,那么2就存在一个入度点 for (int[] info : prerequisites) { edges.get(info[1]).add(info[0]); ++indeg[info[0]]; } Queue<Integer> queue = new LinkedList<Integer>(); // 将所有入度为 0 的节点放入队列中 for (int i = 0; i < numCourses; ++i) { if (indeg[i] == 0) { queue.offer(i); } } //这里看着有点绕 //把对应入度为0的点拿出来放入结果集,且把该点可以走向的点的入度都减1, //减完后满足入度为0的又会被加入到入度为0的集合中 while (!queue.isEmpty()) { // 从队首取出一个节点 int u = queue.poll(); // 放入答案中 result[index++] = u; for (int v: edges.get(u)) { --indeg[v]; // 如果相邻节点 v 的入度为 0,就可以选 v 对应的课程了 if (indeg[v] == 0) { queue.offer(v); } } } //如果数量不等的情况则是因为有环 if (index != numCourses) { return new int[0]; } return result; } } //该解法与上面的是一致的,但是却花费了数倍的时间 //时间20 ms击败11.3% //内存42.1 MB击败94.58% class Solution { public int[] findOrder(int numCourses, int[][] prerequisites) { int[] result = new int[numCourses]; if(numCourses == 0){ return result; } if(prerequisites == null || prerequisites.length == 0){ for(int i = 0; i < numCourses; i++){ result[i] = i; } return result; } int[] indegree = new int[numCourses]; Queue<Integer> zeroDegree = new LinkedList<>(); for(int[] pre : prerequisites){ indegree[pre[0]]++; } for(int i = 0; i < indegree.length; i++){ if(indegree[i] == 0){ zeroDegree.add(i); } } if(zeroDegree.isEmpty()){ return new int[0]; } int index = 0; while( !zeroDegree.isEmpty() ){ int course = zeroDegree.poll(); result[index] = course; index++; for(int[] pre : prerequisites){ if(pre[1] == course){ indegree[pre[0]]--; if(indegree[pre[0]] == 0){ zeroDegree.add(pre[0]); } } } } for(int in : indegree){ if(in != 0){ return new int[0]; } } return result; } }
深度优先搜索的方式:
//时间3 ms击败93.23% //内存42.6 MB击败48.1% //时间复杂度: O(n+m),其中 n 为课程数,m 为先修课程的要求数。 //这其实就是对图进行深度优先搜索的时间复杂度。 //空间复杂度: O(n+m)。 //题目中是以列表形式给出的先修课程关系,为了对图进行深度优先搜索,我们需要存储成邻接表的形式,空间复杂度为 O(n+m)。 //在深度优先搜索的过程中,我们需要最多 O(n) 的栈空间(递归)进行深度优先搜索,并且还需要若干个 O(n) 的空间存储节点状态、最终答案等。 class Solution { // 存储有向图 List<List<Integer>> edges; // 标记每个节点的状态:0=未搜索,1=搜索中,2=已完成 int[] visited; // 用数组来模拟栈,下标 n-1 为栈底,0 为栈顶 int[] result; // 判断有向图中是否有环 boolean valid = true; // 栈下标 int index; public int[] findOrder(int numCourses, int[][] prerequisites) { edges = new ArrayList<List<Integer>>(); for (int i = 0; i < numCourses; ++i) { edges.add(new ArrayList<Integer>()); } visited = new int[numCourses]; result = new int[numCourses]; index = numCourses - 1; for (int[] info : prerequisites) { edges.get(info[1]).add(info[0]); } // 每次挑选一个「未搜索」的节点,开始进行深度优先搜索 for (int i = 0; i < numCourses && valid; ++i) { if (visited[i] == 0) { dfs(i); } } if (!valid) { return new int[0]; } // 如果没有环,那么就有拓扑排序 return result; } public void dfs(int u) { // 将节点标记为「搜索中」 visited[u] = 1; // 搜索其相邻节点 // 只要发现有环,立刻停止搜索 for (int v: edges.get(u)) { // 如果「未搜索」那么搜索相邻节点 if (visited[v] == 0) { dfs(v); if (!valid) { return; } } // 如果「搜索中」说明找到了环 else if (visited[v] == 1) { valid = false; return; } } // 将节点标记为「已完成」 visited[u] = 2; // 将节点入栈 result[index--] = u; } }
【207. 课程表的代码】
//时间4 ms 击败 62.90% //内存42.9 MB 击败 22.49% // 逻辑说明: // 本质上是将每一个节点如果需要一个前置课程,那么入度就会增加1, // 所以一开始是先统计每个节点的入度 // 然后根据入度为0的先学习,学习完后其他可能,对应的前置要-1,如果为零也会被纳入到需要学习的行列 // 直至全部入度都为0,即结束 class Solution { // 存储有向图 List<List<Integer>> edges; // 存储每个节点的入度 int[] indeg; // 存储答案 int[] result; // 答案下标 int index; public boolean canFinish(int numCourses, int[][] prerequisites) { edges = new ArrayList<List<Integer>>(); for (int i = 0; i < numCourses; ++i) { edges.add(new ArrayList<Integer>()); } indeg = new int[numCourses]; result = new int[numCourses]; index = 0; for (int[] info : prerequisites) { edges.get(info[1]).add(info[0]); ++indeg[info[0]]; } Queue<Integer> queue = new LinkedList<Integer>(); // 将所有入度为 0 的节点放入队列中 for (int i = 0; i < numCourses; ++i) { if (indeg[i] == 0) { queue.offer(i); } } while (!queue.isEmpty()) { // 从队首取出一个节点 int u = queue.poll(); // 放入答案中 result[index++] = u; for (int v: edges.get(u)) { --indeg[v]; // 如果相邻节点 v 的入度为 0,就可以选 v 对应的课程了 if (indeg[v] == 0) { queue.offer(v); } } } return index == numCourses; } } //时间3 ms 击败 91.91% //内存42.9 MB 击败 20.20% class Solution { List<List<Integer>> edges; int[] visited; boolean valid = true; public boolean canFinish(int numCourses, int[][] prerequisites) { edges = new ArrayList<List<Integer>>(); for (int i = 0; i < numCourses; ++i) { edges.add(new ArrayList<Integer>()); } visited = new int[numCourses]; for (int[] info : prerequisites) { edges.get(info[1]).add(info[0]); } for (int i = 0; i < numCourses && valid; ++i) { if (visited[i] == 0) { dfs(i); } } return valid; } public void dfs(int u) { visited[u] = 1; for (int v: edges.get(u)) { if (visited[v] == 0) { dfs(v); if (!valid) { return; } } else if (visited[v] == 1) { valid = false; return; } } visited[u] = 2; } } //时间2 ms 击败 99.26% //内存42.8 MB 击败 24.86% class Solution { int[] status; boolean hasCycle = false; List<Integer>[] graph; public boolean canFinish(int numCourses, int[][] prerequisites) { // 0: 未搜索 ; 1: 搜索中 ; 2: 已完成. this.status = new int[numCourses]; this.graph = new ArrayList[numCourses]; for (int i = 0; i < numCourses; i++) graph[i] = new ArrayList<>(); // 建图 for (int[] grid : prerequisites) { graph[grid[1]].add(grid[0]); } for (int i = 0; i < numCourses; i++) { if (status[i] == 0) { dfs(i); if (hasCycle) return false; } } return true; } public void dfs(int u) { if (hasCycle) return; status[u] = 1; for (int v : graph[u]) { if (status[v] == 0) dfs(v); else if (status[v] == 1) { hasCycle = true; return; } } status[u] = 2; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号