剑指 Offer II 111. 计算除法（399. 除法求值）

题目：

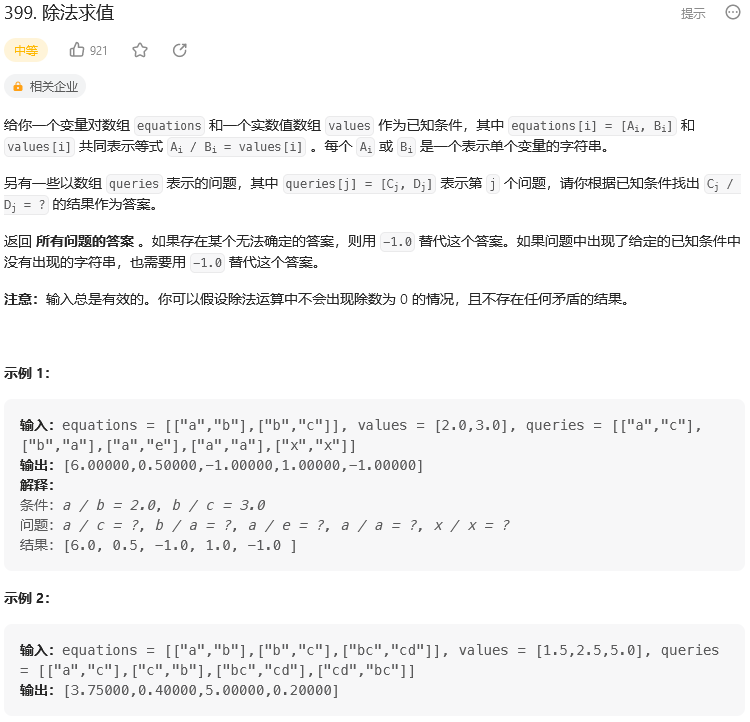
思路：

【0】并查集的方式

【1】广度优先搜索的方式

【2】Floyd 算法的方式

【3】带权并查集的方式

代码展示：

并查集的方式：

//时间0 ms击败100%
//内存40.1 MB击败36.27%
//时间复杂度：O((N+Q)log⁡A)，
//构建并查集 O(Nlog⁡A) ，这里 N 为输入方程 equations 的长度，每一次执行合并操作的时间复杂度是 O(log⁡A)，这里 A 是 equations 里不同字符的个数；
//查询并查集 O(Qlog⁡A)，这里 Q 为查询数组 queries 的长度，每一次查询时执行「路径压缩」的时间复杂度是 O(log⁡A)。
//空间复杂度：O(A)：创建字符与 id 的对应关系 hashMap 长度为 A，并查集底层使用的两个数组 parent 和 weight 存储每个变量的连通分量信息，parent 和 weight 的长度均为 A。

import java.util.HashMap;
import java.util.List;
import java.util.Map;

public class Solution {

    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        int equationsSize = equations.size();

        UnionFind unionFind = new UnionFind(2 * equationsSize);
        // 第 1 步：预处理，将变量的值与 id 进行映射，使得并查集的底层使用数组实现，方便编码
        Map<String, Integer> hashMap = new HashMap<>(2 * equationsSize);
        int id = 0;
        for (int i = 0; i < equationsSize; i++) {
            List<String> equation = equations.get(i);
            String var1 = equation.get(0);
            String var2 = equation.get(1);

            if (!hashMap.containsKey(var1)) {
                hashMap.put(var1, id);
                id++;
            }
            if (!hashMap.containsKey(var2)) {
                hashMap.put(var2, id);
                id++;
            }
            unionFind.union(hashMap.get(var1), hashMap.get(var2), values[i]);
        }

        // 第 2 步：做查询
        int queriesSize = queries.size();
        double[] res = new double[queriesSize];
        for (int i = 0; i < queriesSize; i++) {
            String var1 = queries.get(i).get(0);
            String var2 = queries.get(i).get(1);

            Integer id1 = hashMap.get(var1);
            Integer id2 = hashMap.get(var2);

            if (id1 == null || id2 == null) {
                res[i] = -1.0d;
            } else {
                res[i] = unionFind.isConnected(id1, id2);
            }
        }
        return res;
    }

    private class UnionFind {

        private int[] parent;

        /**
         * 指向的父结点的权值
         */
        private double[] weight;


        public UnionFind(int n) {
            this.parent = new int[n];
            this.weight = new double[n];
            for (int i = 0; i < n; i++) {
                parent[i] = i;
                weight[i] = 1.0d;
            }
        }

        public void union(int x, int y, double value) {
            int rootX = find(x);
            int rootY = find(y);
            if (rootX == rootY) {
                return;
            }

            parent[rootX] = rootY;
            // 关系式的推导请见「参考代码」下方的示意图
            weight[rootX] = weight[y] * value / weight[x];
        }

        /**
         * 路径压缩
         *
         * @param x
         * @return 根结点的 id
         */
        public int find(int x) {
            if (x != parent[x]) {
                int origin = parent[x];
                parent[x] = find(parent[x]);
                weight[x] *= weight[origin];
            }
            return parent[x];
        }

        public double isConnected(int x, int y) {
            int rootX = find(x);
            int rootY = find(y);
            if (rootX == rootY) {
                return weight[x] / weight[y];
            } else {
                return -1.0d;
            }
        }
    }
}

 

广度优先搜索的方式：

//时间1 ms击败53.43%
//内存40.2 MB击败25.10%
//时间复杂度：O(ML+Q*(L+M))，其中 M 为边的数量，Q 为询问的数量，L 为字符串的平均长度。
//构建图时，需要处理 M 条边，每条边都涉及到 O(L) 的字符串比较；
//处理查询时，每次查询首先要进行一次 O(L) 的比较，然后至多遍历 O(M) 条边。
//空间复杂度：O(NL+M)，其中 N 为点的数量，M 为边的数量，L 为字符串的平均长度。
//为了将每个字符串映射到整数，需要开辟空间为 O(NL) 的哈希表；
//随后，需要花费 O(M) 的空间存储每条边的权重；
//处理查询时，还需要 O(N) 的空间维护访问队列。
//最终，总的复杂度为 O(NL+M+N)=O(NL+M)。
class Solution {
    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        int nvars = 0;
        Map<String, Integer> variables = new HashMap<String, Integer>();

        int n = equations.size();
        for (int i = 0; i < n; i++) {
            if (!variables.containsKey(equations.get(i).get(0))) {
                variables.put(equations.get(i).get(0), nvars++);
            }
            if (!variables.containsKey(equations.get(i).get(1))) {
                variables.put(equations.get(i).get(1), nvars++);
            }
        }

        // 对于每个点，存储其直接连接到的所有点及对应的权值
        List<Pair>[] edges = new List[nvars];
        for (int i = 0; i < nvars; i++) {
            edges[i] = new ArrayList<Pair>();
        }
        for (int i = 0; i < n; i++) {
            int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));
            edges[va].add(new Pair(vb, values[i]));
            edges[vb].add(new Pair(va, 1.0 / values[i]));
        }

        int queriesCount = queries.size();
        double[] ret = new double[queriesCount];
        for (int i = 0; i < queriesCount; i++) {
            List<String> query = queries.get(i);
            double result = -1.0;
            if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {
                int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));
                if (ia == ib) {
                    result = 1.0;
                } else {
                    Queue<Integer> points = new LinkedList<Integer>();
                    points.offer(ia);
                    double[] ratios = new double[nvars];
                    Arrays.fill(ratios, -1.0);
                    ratios[ia] = 1.0;

                    while (!points.isEmpty() && ratios[ib] < 0) {
                        int x = points.poll();
                        for (Pair pair : edges[x]) {
                            int y = pair.index;
                            double val = pair.value;
                            if (ratios[y] < 0) {
                                ratios[y] = ratios[x] * val;
                                points.offer(y);
                            }
                        }
                    }
                    result = ratios[ib];
                }
            }
            ret[i] = result;
        }
        return ret;
    }
}

class Pair {
    int index;
    double value;

    Pair(int index, double value) {
        this.index = index;
        this.value = value;
    }
}

Floyd 算法的方式

//时间1 ms击败82.38%
//内存40.1 MB击败40.15%
class Solution {
    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        int nvars = 0;
        Map<String, Integer> variables = new HashMap<String, Integer>();

        int n = equations.size();
        for (int i = 0; i < n; i++) {
            if (!variables.containsKey(equations.get(i).get(0))) {
                variables.put(equations.get(i).get(0), nvars++);
            }
            if (!variables.containsKey(equations.get(i).get(1))) {
                variables.put(equations.get(i).get(1), nvars++);
            }
        }
        double[][] graph = new double[nvars][nvars];
        for (int i = 0; i < nvars; i++) {
            Arrays.fill(graph[i], -1.0);
        }
        for (int i = 0; i < n; i++) {
            int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));
            graph[va][vb] = values[i];
            graph[vb][va] = 1.0 / values[i];
        }

        for (int k = 0; k < nvars; k++) {
            for (int i = 0; i < nvars; i++) {
                for (int j = 0; j < nvars; j++) {
                    if (graph[i][k] > 0 && graph[k][j] > 0) {
                        graph[i][j] = graph[i][k] * graph[k][j];
                    }
                }
            }
        }

        int queriesCount = queries.size();
        double[] ret = new double[queriesCount];
        for (int i = 0; i < queriesCount; i++) {
            List<String> query = queries.get(i);
            double result = -1.0;
            if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {
                int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));
                if (graph[ia][ib] > 0) {
                    result = graph[ia][ib];
                }
            }
            ret[i] = result;
        }
        return ret;
    }
}

 

带权并查集的方式

//时间0 ms击败100%
//内存40.1 MB击败51.29%
class Solution {
    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        int nvars = 0;
        Map<String, Integer> variables = new HashMap<String, Integer>();

        int n = equations.size();
        for (int i = 0; i < n; i++) {
            if (!variables.containsKey(equations.get(i).get(0))) {
                variables.put(equations.get(i).get(0), nvars++);
            }
            if (!variables.containsKey(equations.get(i).get(1))) {
                variables.put(equations.get(i).get(1), nvars++);
            }
        }
        int[] f = new int[nvars];
        double[] w = new double[nvars];
        Arrays.fill(w, 1.0);
        for (int i = 0; i < nvars; i++) {
            f[i] = i;
        }

        for (int i = 0; i < n; i++) {
            int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));
            merge(f, w, va, vb, values[i]);
        }
        int queriesCount = queries.size();
        double[] ret = new double[queriesCount];
        for (int i = 0; i < queriesCount; i++) {
            List<String> query = queries.get(i);
            double result = -1.0;
            if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {
                int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));
                int fa = findf(f, w, ia), fb = findf(f, w, ib);
                if (fa == fb) {
                    result = w[ia] / w[ib];
                }
            }
            ret[i] = result;
        }
        return ret;
    }

    public void merge(int[] f, double[] w, int x, int y, double val) {
        int fx = findf(f, w, x);
        int fy = findf(f, w, y);
        f[fx] = fy;
        w[fx] = val * w[y] / w[x];
    }

    public int findf(int[] f, double[] w, int x) {
        if (f[x] != x) {
            int father = findf(f, w, f[x]);
            w[x] = w[x] * w[f[x]];
            f[x] = father;
        }
        return f[x];
    }
}