剑指 Offer II 086. 分割回文子字符串（131. 分割回文串）

题目：

 

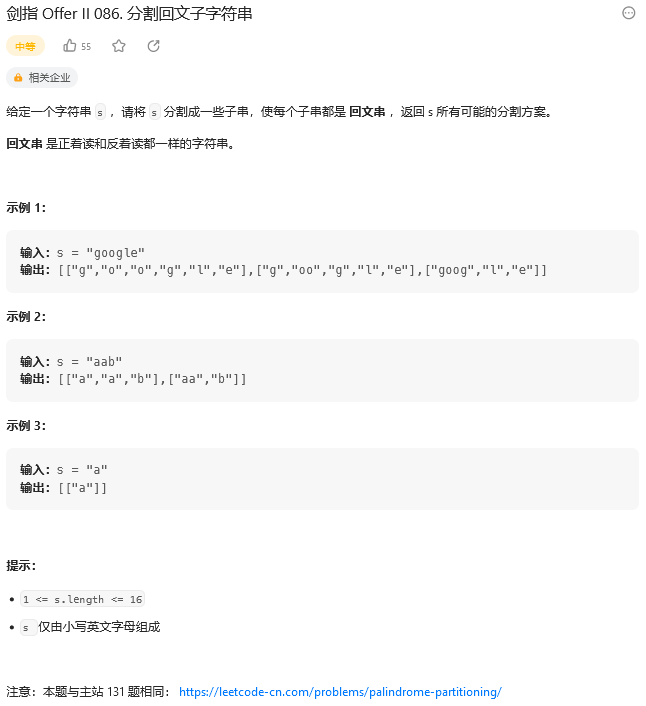
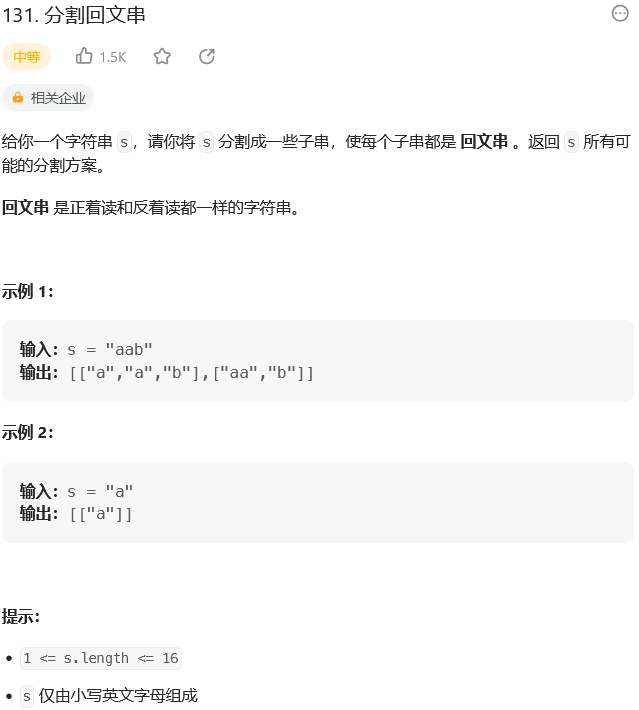
思路：

【1】回溯算法的方式，本题的递归树模型是一棵多叉树；

 

 

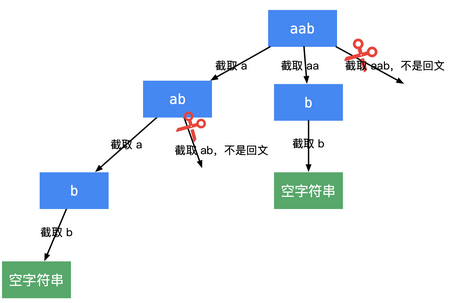
【2】回溯 + 动态规划预处理的方式

【3】回溯 + 记忆化搜索的方式

代码展示：

回溯算法的方式：

//时间8 ms击败62.40%
//内存53.2 MB击败96.99%
class Solution {
    public List<List<String>> partition(String s) {
        int len = s.length();
        List<List<String>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        // Stack 这个类 Java 的文档里推荐写成 Deque<Integer> stack = new ArrayDeque<Integer>();
        // 注意：只使用 stack 相关的接口
        Deque<String> stack = new ArrayDeque<>();
        char[] charArray = s.toCharArray();
        dfs(charArray, 0, len, stack, res);
        return res;
    }

    /**
     * @param charArray
     * @param index     起始字符的索引
     * @param len       字符串 s 的长度，可以设置为全局变量
     * @param path      记录从根结点到叶子结点的路径
     * @param res       记录所有的结果
     */
    private void dfs(char[] charArray, int index, int len, Deque<String> path, List<List<String>> res) {
        if (index == len) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = index; i < len; i++) {
            // 因为截取字符串是消耗性能的，因此，采用传子串下标的方式判断一个子串是否是回文子串
            if (!checkPalindrome(charArray, index, i)) {
                continue;
            }
            path.addLast(new String(charArray, index, i + 1 - index));
            dfs(charArray, i + 1, len, path, res);
            path.removeLast();
        }
    }

    /**
     * 这一步的时间复杂度是 O(N)，优化的解法是，先采用动态规划，把回文子串的结果记录在一个表格里
     *
     * @param charArray
     * @param left      子串的左边界，可以取到
     * @param right     子串的右边界，可以取到
     * @return
     */
    private boolean checkPalindrome(char[] charArray, int left, int right) {
        while (left < right) {
            if (charArray[left] != charArray[right]) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

 

回溯 + 动态规划预处理的方式：

//时间6 ms击败99.10%
//内存53.5 MB击败76.28%
class Solution {
    boolean[][] f;
    List<List<String>> ret = new ArrayList<List<String>>();
    List<String> ans = new ArrayList<String>();
    int n;

    public List<List<String>> partition(String s) {
        n = s.length();
        f = new boolean[n][n];
        for (int i = 0; i < n; ++i) {
            Arrays.fill(f[i], true);
        }

        for (int i = n - 1; i >= 0; --i) {
            for (int j = i + 1; j < n; ++j) {
                f[i][j] = (s.charAt(i) == s.charAt(j)) && f[i + 1][j - 1];
            }
        }

        dfs(s, 0);
        return ret;
    }

    public void dfs(String s, int i) {
        if (i == n) {
            ret.add(new ArrayList<String>(ans));
            return;
        }
        for (int j = i; j < n; ++j) {
            if (f[i][j]) {
                ans.add(s.substring(i, j + 1));
                dfs(s, j + 1);
                ans.remove(ans.size() - 1);
            }
        }
    }
}

 

回溯 + 记忆化搜索的方式：

//时间6 ms击败99.10%
//内存53.6 MB击败69.98%
class Solution {
    int[][] f;
    List<List<String>> ret = new ArrayList<List<String>>();
    List<String> ans = new ArrayList<String>();
    int n;

    public List<List<String>> partition(String s) {
        n = s.length();
        f = new int[n][n];

        dfs(s, 0);
        return ret;
    }

    public void dfs(String s, int i) {
        if (i == n) {
            ret.add(new ArrayList<String>(ans));
            return;
        }
        for (int j = i; j < n; ++j) {
            if (isPalindrome(s, i, j) == 1) {
                ans.add(s.substring(i, j + 1));
                dfs(s, j + 1);
                ans.remove(ans.size() - 1);
            }
        }
    }

    // 记忆化搜索中，f[i][j] = 0 表示未搜索，1 表示是回文串，-1 表示不是回文串
    public int isPalindrome(String s, int i, int j) {
        if (f[i][j] != 0) {
            return f[i][j];
        }
        if (i >= j) {
            f[i][j] = 1;
        } else if (s.charAt(i) == s.charAt(j)) {
            f[i][j] = isPalindrome(s, i + 1, j - 1);
        } else {
            f[i][j] = -1;
        }
        return f[i][j];
    }
}