剑指 Offer II 050. 向下的路径节点之和(437. 路径总和 III)
题目:
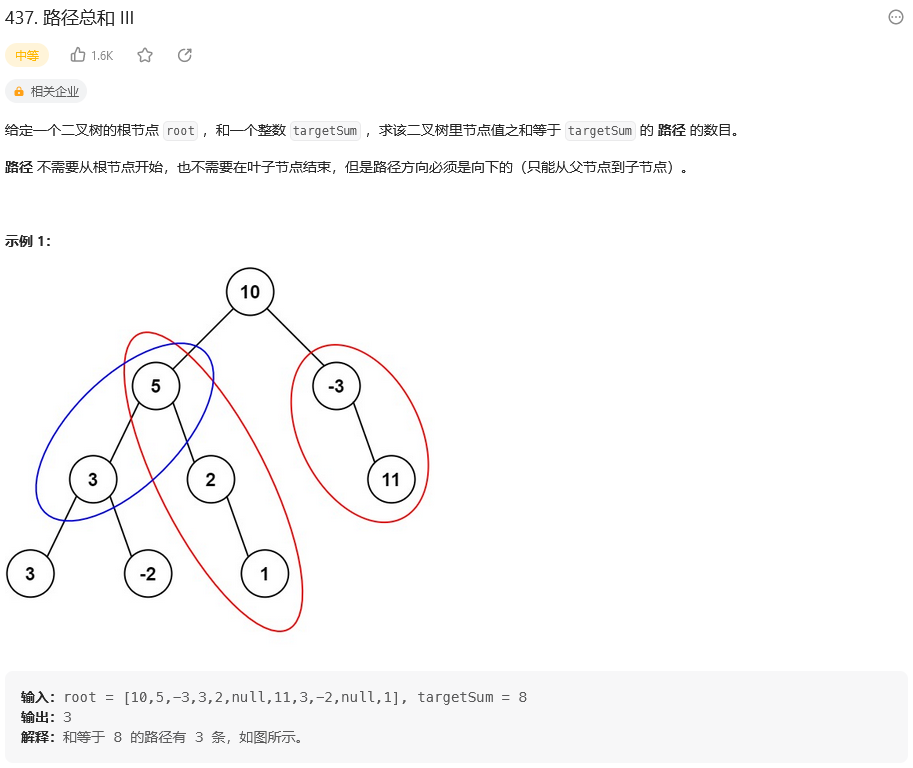

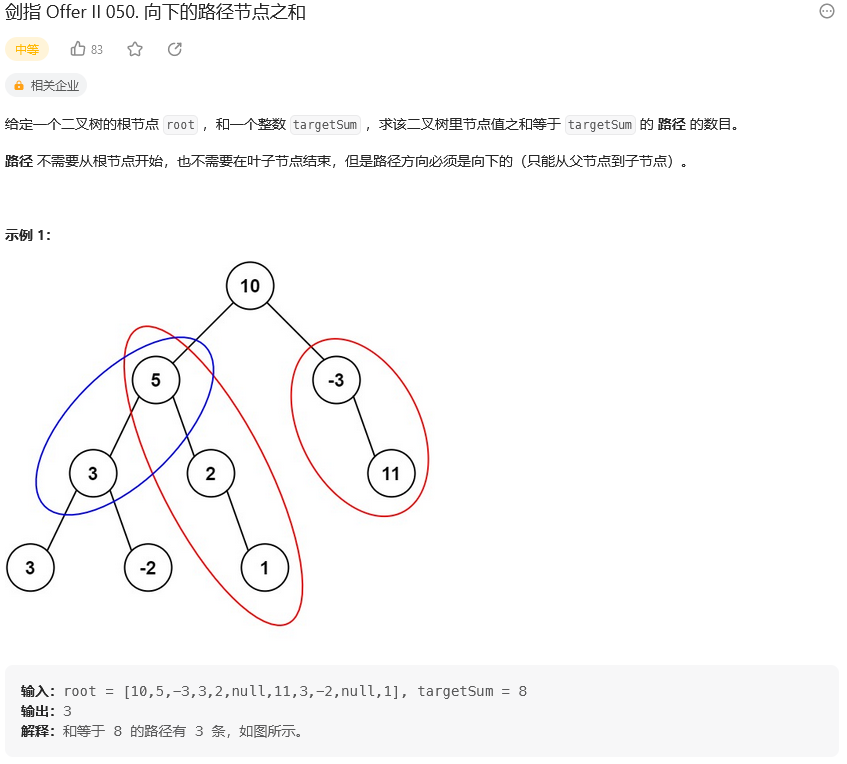

思路:
【1】深度优先搜索
【2】前缀和的方式
代码展示:
前缀和的方式:
//时间2 ms击败100% //内存40.9 MB击败75.50% //时间复杂度:O(N),其中 N 为二叉树中节点的个数。利用前缀和只需遍历一次二叉树即可。 //空间复杂度:O(N)。 //树上问题转换一维问题:求解从原始起点(根节点)到当前节点 b 的路径中,有多少节点 a 满足 sum[a...b]=targetSum, //由于从原始起点(根节点)到当前节点的路径唯一,因此这其实是一个「一维前缀和」问题。 class Solution { public int pathSum(TreeNode root, int targetSum) { Map<Long, Integer> prefix = new HashMap<Long, Integer>(); prefix.put(0L, 1); return dfs(root, prefix, 0, targetSum); } public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) { if (root == null) return 0; int ret = 0; curr += root.val; //如果存在差值的次数就代表则有多少条路径是可行的 ret = prefix.getOrDefault(curr - targetSum, 0); //这个总数出现的次数要加1,因为如果能到达这个总数的话,位置越多,代表可选越多 prefix.put(curr, prefix.getOrDefault(curr, 0) + 1); ret += dfs(root.left, prefix, curr, targetSum); ret += dfs(root.right, prefix, curr, targetSum); //由于我们只能统计往下的路径,但是树的遍历会同时搜索两个方向的子树。 // 因此我们应当在搜索完以某个节点为根的左右子树之后,应当回溯地将路径总和从哈希表中删除,防止统计到跨越两个方向的路径。 prefix.put(curr, prefix.getOrDefault(curr, 0) - 1); return ret; } }
深度优先搜索:
//时间37 ms击败8.72% //内存41.1 MB击败56.88% //时间复杂度:O(N^2),其中 N 为该二叉树节点的个数。 //对于每一个节点,求以该节点为起点的路径数目时,则需要遍历以该节点为根节点的子树的所有节点,因此求该路径所花费的最大时间为 O(N), //我们会对每个节点都求一次以该节点为起点的路径数目,因此时间复杂度为 O(N^2)。 //空间复杂度:O(N),考虑到递归需要在栈上开辟空间。 /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public int pathSum(TreeNode root, int targetSum) { if (root == null) { return 0; } int ret = rootSum(root, targetSum); ret += pathSum(root.left, targetSum); ret += pathSum(root.right, targetSum); return ret; } public int rootSum(TreeNode root, long targetSum) { int ret = 0; if (root == null) { return 0; } int val = root.val; if (val == targetSum) { ret++; } ret += rootSum(root.left, targetSum - val); ret += rootSum(root.right, targetSum - val); return ret; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号