剑指 Offer II 100. 三角形中最小路径之和（120. 三角形最小路径和）

题目：

 

 

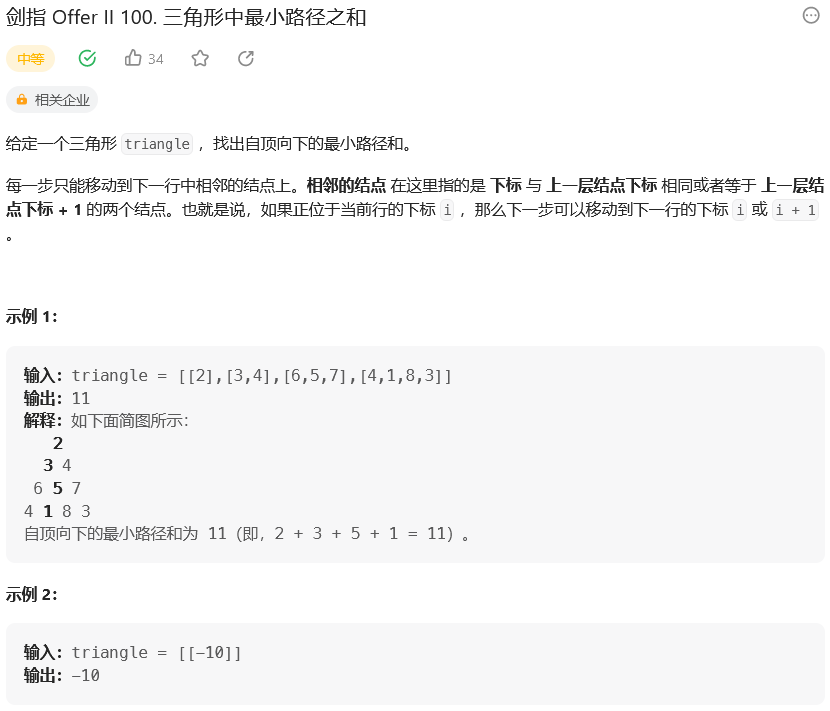
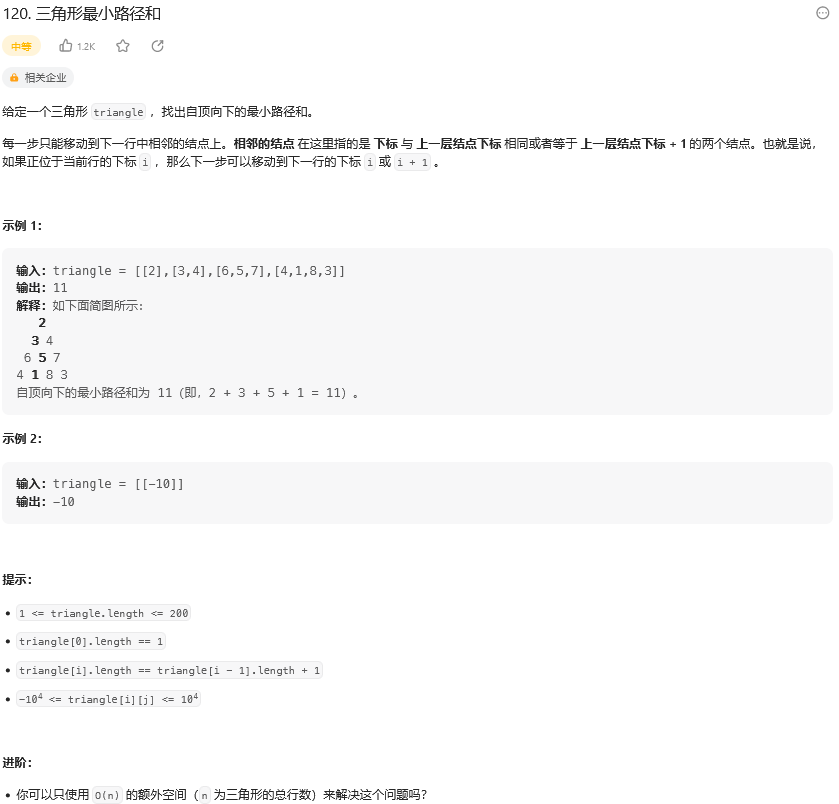
思路：

【1】动态规划的方式

代码展示：

针对枚举进行空间复杂度的降低（空间优化）：

//输入的示例（将每一行的左端对齐，那么会形成一个等腰直角三角形，也可以说像是梯形）
        //[2]
        //[3,4]
        //[6,5,7]
        //[4,1,8,3]
        int n = triangle.size();
        //只取一层的变量来进行更替
        int[] f = new int[n];
        //由于第一层只有一个数所以直接赋值
        f[0] = triangle.get(0).get(0);
        //从第二层开始遍历
        for (int i = 1; i < n; ++i) {
            //由于每到下一层其实都会多一个数，而这个数恰好与上一层的最后一个数有关，先赋值（因为不影响其他值）
            f[i] = f[i - 1] + triangle.get(i).get(i);
            //然后到了要覆盖的地方
            //如一开始的[2,0,0,0]
            //到后面的[5,6,0,0]
            //先是上面填入了7，形成[5,6,13,0],再到填入5,因为到5可以有两条路走，其中5+5最小，故形成[5,10,13,0]
            for (int j = i - 1; j > 0; --j) {
                f[j] = Math.min(f[j - 1], f[j]) + triangle.get(i).get(j);
            }
            //最后填入6，形成[11,10,13,0]
            f[0] += triangle.get(i).get(0);
        }
        int minTotal = f[0];
        for (int i = 1; i < n; ++i) {
            minTotal = Math.min(minTotal, f[i]);
        }
        return minTotal;

 

动态规划枚举出所有结果：

//时间2 ms击败95.53%
//内存41.4 MB击败53.87%
//时间复杂度：O(n^2)，其中 n 是三角形的行数。
//空间复杂度：O(n^2)。我们需要一个 n∗n 的二维数组存放所有的状态。
class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        //输入的示例（将每一行的左端对齐，那么会形成一个等腰直角三角形，也可以说像是梯形）
        //[2]
        //[3,4]
        //[6,5,7]
        //[4,1,8,3]
        int n = triangle.size();
        //记录动态规划的结果（即每个位置枚举的结果）
        int[][] f = new int[n][n];
        f[0][0] = triangle.get(0).get(0);
        for (int i = 1; i < n; ++i) {
            //由于是梯形，所以第一列只能往上加
            f[i][0] = f[i - 1][0] + triangle.get(i).get(0);
            for (int j = 1; j < i; ++j) {
                f[i][j] = Math.min(f[i - 1][j - 1], f[i - 1][j]) + triangle.get(i).get(j);
            }
            //最后的数值和第一列的一样都是只能加一个数的
            f[i][i] = f[i - 1][i - 1] + triangle.get(i).get(i);
        }
        //汇总到最后一行，然后将最后一行的最小值取出
        int minTotal = f[n - 1][0];
        for (int i = 1; i < n; ++i) {
            minTotal = Math.min(minTotal, f[n - 1][i]);
        }
        return minTotal;
    }
}

 如果允许在原本的数组上进行修改的话：

//时间6 ms击败11.1%
//内存41.6 MB击败20.82%
//时间复杂度：O(n^2)，其中 n 是三角形的行数。
//空间复杂度：O(1)。由于在原本的数组上面进行修改，而原本的数组是不纳入到空间复杂度的统计的。
class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        //输入的示例（将每一行的左端对齐，那么会形成一个等腰直角三角形，也可以说像是梯形）
        //[2]
        //[3,4]
        //[6,5,7]
        //[4,1,8,3]
        int n = triangle.size();
        //记录动态规划的结果（即每个位置枚举的结果）
        int[][] f = new int[n][n];
        f[0][0] = triangle.get(0).get(0);
        for (int i = 1; i < n; ++i) {
            //由于是梯形，所以第一列只能往上加
            f[i][0] = f[i - 1][0] + triangle.get(i).get(0);
            for (int j = 1; j < i; ++j) {
                f[i][j] = Math.min(f[i - 1][j - 1], f[i - 1][j]) + triangle.get(i).get(j);
            }
            //最后的数值和第一列的一样都是只能加一个数的
            f[i][i] = f[i - 1][i - 1] + triangle.get(i).get(i);
        }
        //汇总到最后一行，然后将最后一行的最小值取出
        int minTotal = f[n - 1][0];
        for (int i = 1; i < n; ++i) {
            minTotal = Math.min(minTotal, f[n - 1][i]);
        }
        return minTotal;
    }
}