剑指 Offer II 084. 含有重复元素集合的全排列 （47. 全排列 II）

题目：

 

 

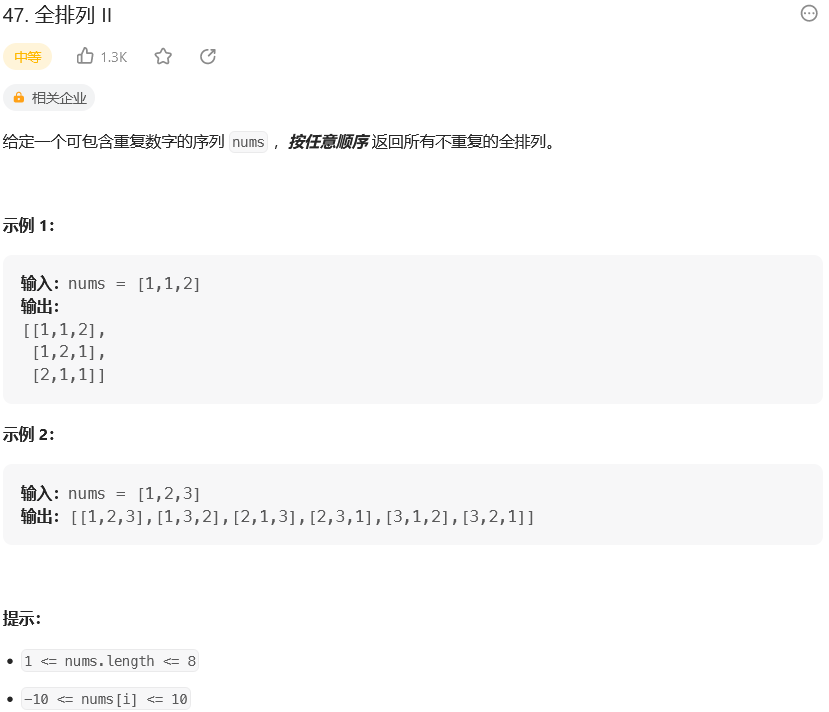
思路：

【1】回溯的方式

代码展示：

//时间4 ms击败12.21%
//内存42 MB击败82.83%
//时间复杂度：O(n×n!)，其中 n 为序列的长度。
//空间复杂度：O(n)。我们需要 O(n) 的记录哈希表，同时在递归的时候栈深度会达到 O(n)，因此总空间复杂度为 O(n+n)=O(2n)=O(n)。
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        HashMap<Integer, Integer> freq = new HashMap<>();
        for (int num : nums) {
            freq.put(num,freq.getOrDefault(num,0)+1);
        }
        Deque<Integer> path = new ArrayDeque<>();
        dfs(freq,nums.length,path,res);
        return res;
    }

    private void dfs(HashMap<Integer, Integer> candidates, int len, Deque<Integer> path, List<List<Integer>> res) {
        if (len == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (Integer key : candidates.keySet()){
            if(candidates.get(key) <= 0) continue;
            path.addLast(key);
            candidates.put(key,candidates.get(key)-1);
            //进行递归
            dfs(candidates, len - 1, path, res);
            // 状态重置
            candidates.put(key,candidates.get(key)+1);
            path.removeLast();
        }
    }
}

//使用数组尝试替代哈希表提高运行速度
//时间1 ms击败99.52%
//内存42.2 MB击败53.24%
class Solution {
    boolean[] vis;

    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        List<Integer> perm = new ArrayList<Integer>();
        vis = new boolean[nums.length];
        Arrays.sort(nums);
        backtrack(nums, ans, 0, perm);
        return ans;
    }

    public void backtrack(int[] nums, List<List<Integer>> ans, int idx, List<Integer> perm) {
        if (idx == nums.length) {
            ans.add(new ArrayList<Integer>(perm));
            return;
        }
        for (int i = 0; i < nums.length; ++i) {
            if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
                continue;
            }
            perm.add(nums[i]);
            vis[i] = true;
            backtrack(nums, ans, idx + 1, perm);
            vis[i] = false;
            perm.remove(idx);
        }
    }
}

//又或者这样
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        dfs(nums, res, 0);
        return res;
    }

    private void dfs(int[] nums, List<List<Integer>> res, int index) {
        if (index == nums.length) {
            List<Integer> path = new ArrayList<>();
            for (int num : nums) {
                path.add(num);
            }
            res.add(path);
            return;
        }
        boolean[] used = new boolean[21];
        for (int i = index; i < nums.length; i++) {
            if (used[nums[i] + 10])
                continue;
            used[nums[i] + 10] = true;
            swap(nums, i, index);
            dfs(nums, res, index + 1);
            swap(nums, i, index);
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}