剑指 Offer II 080. 含有 k 个元素的组合（77. 组合）

题目：

 

思路：

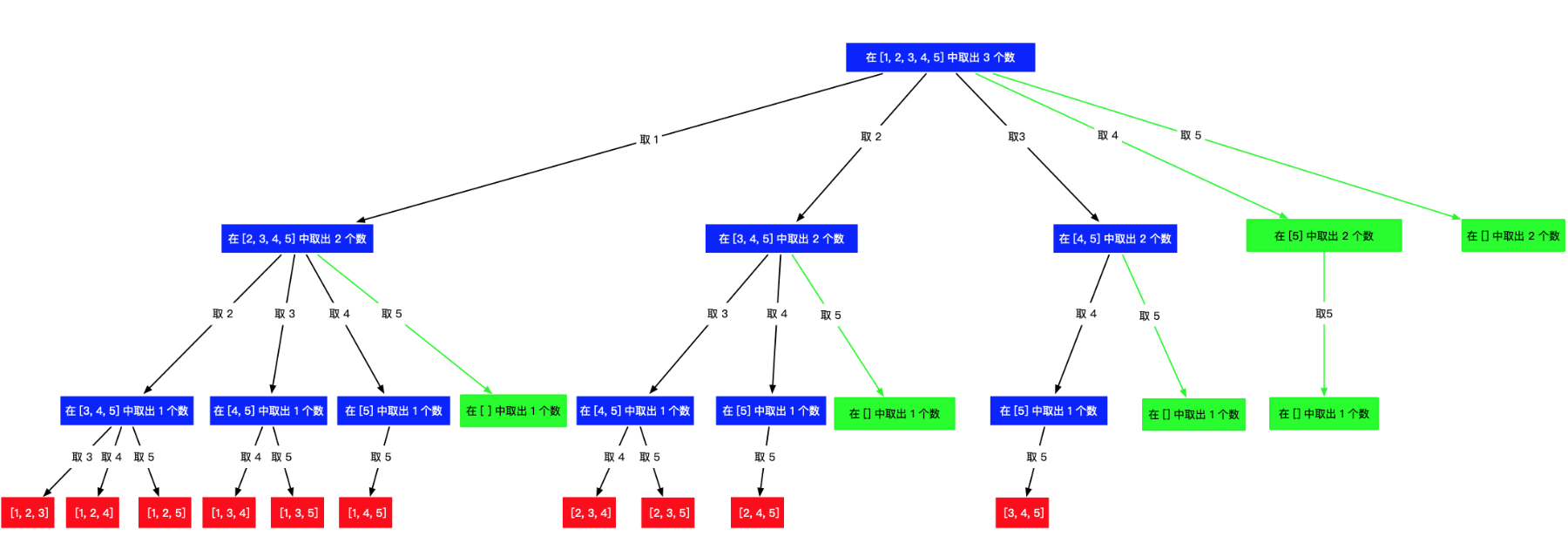
【1】利用回溯的方式：

 

【2】非递归（字典序法）实现组合型枚举（未理解）

代码展示：

非递归（字典序法）实现组合型枚举的方式：

//时间6 ms击败57.94%
//内存42.8 MB击败45.2%
class Solution {
    List<Integer> temp = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> combine(int n, int k) {
        List<Integer> temp = new ArrayList<Integer>();
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        // 初始化
        // 将 temp 中 [0, k - 1] 每个位置 i 设置为 i + 1，即 [0, k - 1] 存 [1, k]
        // 末尾加一位 n + 1 作为哨兵
        for (int i = 1; i <= k; ++i) {
            temp.add(i);
        }
        temp.add(n + 1);
        
        int j = 0;
        while (j < k) {
            ans.add(new ArrayList<Integer>(temp.subList(0, k)));
            j = 0;
            // 寻找第一个 temp[j] + 1 != temp[j + 1] 的位置 t
            // 我们需要把 [0, t - 1] 区间内的每个位置重置成 [1, t]
            while (j < k && temp.get(j) + 1 == temp.get(j + 1)) {
                temp.set(j, j + 1);
                ++j;
            }
            // j 是第一个 temp[j] + 1 != temp[j + 1] 的位置
            temp.set(j, temp.get(j) + 1);
        }
        return ans;
    }
}

 

利用回溯的方式：

//时间24 ms击败10.8%
//内存43.1 MB击败13.83%
//回溯的方式是利用了树的概念，通过选或者不选来决定是否纳入到集合数组中
class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = begin; i <= n; i++) {
            path.addLast(i);
            dfs(n, k, i + 1, path, res);
            path.removeLast();
        }
    }
}

//剪枝的优化
//时间1 ms击败99.98%
//内存42.9 MB击败26.69%
//在回溯过程中剪枝是很重要的，因为可以大大的节约运行的时间
//首先剪枝的有，当剩下的数据不足以组成一个想要的集合的时候，其实这部分就没有必要继续浪费时间的遍历下去
//所以剪枝过程就是：把 i <= n 改成 i <= n - (k - path.size()) + 1 ；
class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = begin; i <= n - (k - path.size()) + 1; i++) {
            path.addLast(i);
            dfs(n, k, i + 1, path, res);
            path.removeLast();
        }
    }
}