剑指 Offer II 082. 含有重复元素集合的组合（40. 组合总和 II）

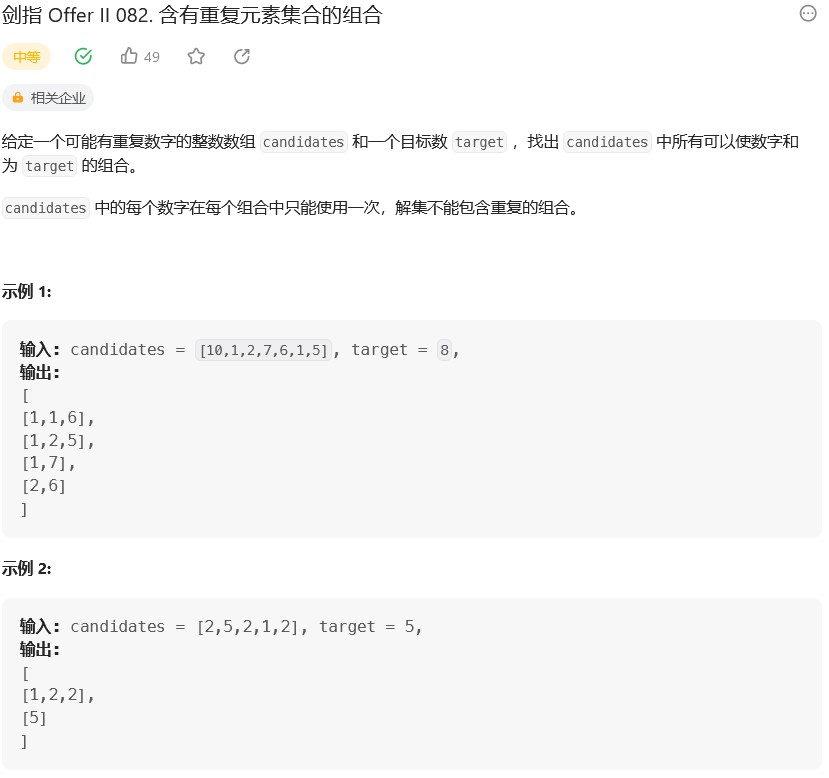
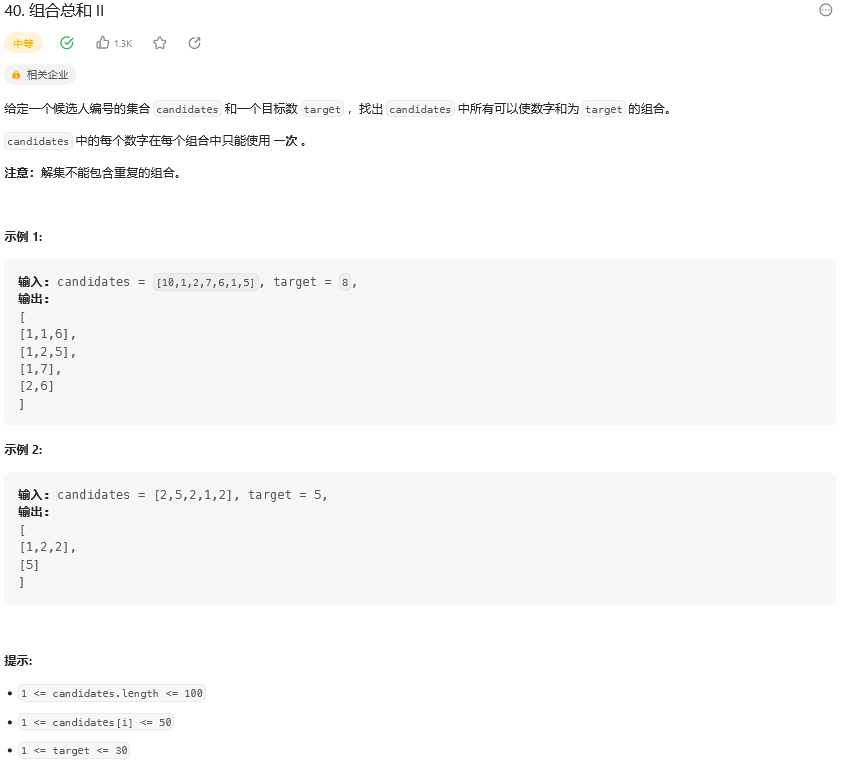
题目：

 

 

思路：

【1】借鉴  剑指 Offer II 081. 允许重复选择元素的组合（39. 组合总和）这道题。首先先从题目看会发现高度重合，区别在于，一个可以重复选，一个不可以重复选，其次是一个是去重的数组，一个是不去重的数组。那么改起来也很简单。

【2】先对数组进行去重，再进行回溯的方式

代码展示：

先对数组进行去重，再进行回溯的方式：

//时间3 ms击败76.64%
//内存41.7 MB击败74.78%
class Solution {
    List<int[]> freq = new ArrayList<int[]>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    List<Integer> sequence = new ArrayList<Integer>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        for (int num : candidates) {
            int size = freq.size();
            if (freq.isEmpty() || num != freq.get(size - 1)[0]) {
                freq.add(new int[]{num, 1});
            } else {
                ++freq.get(size - 1)[1];
            }
        }
        dfs(0, target);
        return ans;
    }

    public void dfs(int pos, int rest) {
        if (rest == 0) {
            ans.add(new ArrayList<Integer>(sequence));
            return;
        }
        if (pos == freq.size() || rest < freq.get(pos)[0]) {
            return;
        }

        dfs(pos + 1, rest);

        int most = Math.min(rest / freq.get(pos)[0], freq.get(pos)[1]);
        for (int i = 1; i <= most; ++i) {
            sequence.add(freq.get(pos)[0]);
            dfs(pos + 1, rest - i * freq.get(pos)[0]);
        }
        for (int i = 1; i <= most; ++i) {
            sequence.remove(sequence.size() - 1);
        }
    }
}

 

借鉴进行修改的方式：

//时间4 ms击败61.9%
//内存41.7 MB击败66.86%
class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }
        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, res);
        return res;
    }

    /**
     * @param candidates 候选数组
     * @param begin      搜索起点
     * @param len        冗余变量，是 candidates 里的属性，可以不传
     * @param target     每减去一个元素，目标值变小
     * @param path       从根结点到叶子结点的路径，是一个栈
     * @param res        结果集列表
     */
    private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
        // target 为负数和 0 的时候不再产生新的孩子结点
        if (target < 0) {
            return;
        }
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 重点理解这里从 begin 开始搜索的语意
        for (int i = begin; i < len; i++) {
            //其次这里也是为了组合去重，因为表示在树的同一层中只会出现该数字一次
            //避免 [10,1,2,7,6,1,5] 这种会出现两个 [1,7]的情况
            if(i > begin && candidates[i] == candidates[i-1]) continue;
            path.addLast(candidates[i]);

            // 注意：由于每一个不元素可以重复使用，下一轮搜索的起点是 i + 1。
            dfs(candidates, i + 1, len, target - candidates[i], path, res);

            // 状态重置
            path.removeLast();
        }
    }
}