剑指 Offer II 076. 数组中的第 k 大的数字（215. 数组中的第K个最大元素）

题目：

 

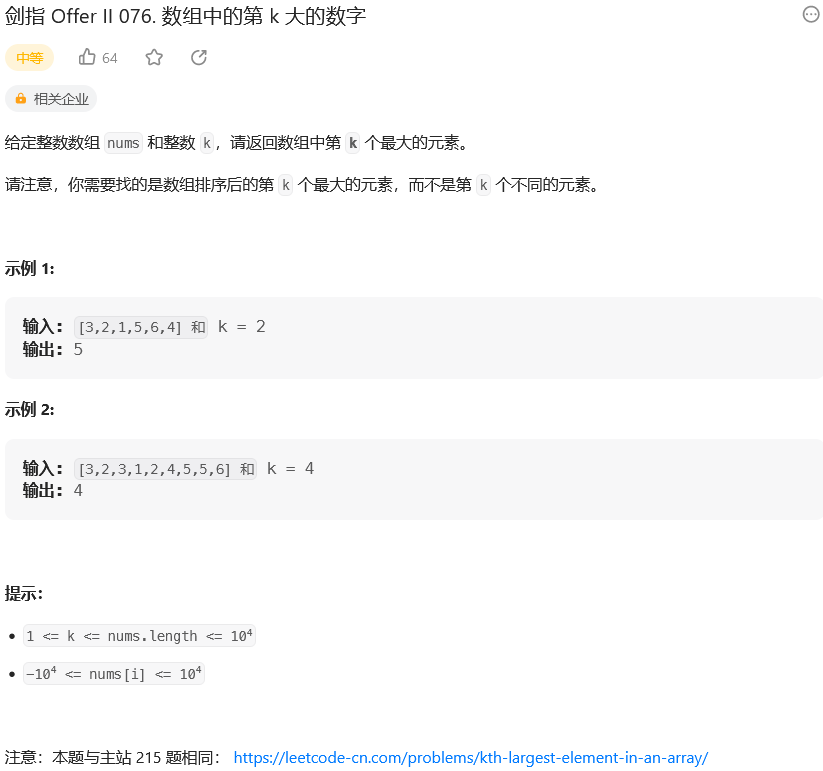
思路：

【0】这道题怎么说呢，不算难，考察的就是能不能默写快排和堆排，说直白点就是要去记，去背，要回默写，其他的没那么重要。

【1】堆排序

【2】快速排序

【3】基于哈希表的方式

代码展示：

基于哈希表的方式：

//时间1 ms击败94.61%
//内存41.6 MB击败53.84%
class Solution {
    public int findKthLargest(int[] nums, int k) {
        int min=nums[0];
        int max=nums[0];
        for(int num:nums){
            if(num<min){
                min=num;
            }
            if(num>max){
                max=num;
            }
        }
        int[] hash=new int[max-min+1];
        for(int num:nums){
            hash[num-min]++;
        }
        for(int i=max-min;i>=0;i--){
            k-=hash[i];
            if(k<=0){
                return i+min;
            }
        }
        return nums[0];
    }
}

 

快速排序的方式：

// 利用内置的排序
//时间23 ms击败54.77%
//内存48.9 MB击败60.47%
class Solution {
    public int findKthLargest(int[] nums, int k) {
        Arrays.sort(nums);
        return nums[nums.length-k];
    }
}

// 自己去实现的快速排序
//时间4 ms击败96.97%
//内存49 MB击败52.5%
class Solution {
    Random random = new Random();

    public int findKthLargest(int[] nums, int k) {
        return quickSelect(nums, 0, nums.length - 1, nums.length - k);
    }

    public int quickSelect(int[] a, int l, int r, int index) {
        int q = randomPartition(a, l, r);
        if (q == index) {
            return a[q];
        } else {
            return q < index ? quickSelect(a, q + 1, r, index) : quickSelect(a, l, q - 1, index);
        }
    }

    public int randomPartition(int[] a, int l, int r) {
        int i = random.nextInt(r - l + 1) + l;
        swap(a, i, r);
        return partition(a, l, r);
    }

    public int partition(int[] a, int l, int r) {
        int x = a[r], i = l - 1;
        for (int j = l; j < r; ++j) {
            if (a[j] <= x) {
                swap(a, ++i, j);
            }
        }
        swap(a, i + 1, r);
        return i + 1;
    }

    public void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

 

堆排序的方式：

// 利用内置的优先队列（里面已经实现了堆排序）
//时间57 ms击败18.90%
//内存51.3 MB击败9.55%
class Solution {
    public int findKthLargest(int[] nums, int k) {
//        PriorityQueue<Integer> queue = new PriorityQueue<Integer>(new Comparator<Integer>() {
//            @Override
//            public int compare(Integer o1, Integer o2) {
//                return o1 - o2;
//            }
//        });
        PriorityQueue<Integer> queue = new PriorityQueue<Integer>((o1, o2) -> o2 - o1);
        for (int num : nums){
            queue.add(num);
        }
        for (int i = 0; i < k-1; i++){
            queue.poll();
        }
        return queue.poll();
    }
}

// 自己去实现的堆排序
//时间2 ms击败72.67%
//内存41.6 MB击败43.26%
class Solution {
    public int findKthLargest(int[] nums, int k) {
        int heapSize = nums.length;
        buildMaxHeap(nums, heapSize);
        for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {
            swap(nums, 0, i);
            --heapSize;
            maxHeapify(nums, 0, heapSize);
        }
        return nums[0];
    }

    public void buildMaxHeap(int[] a, int heapSize) {
        for (int i = heapSize / 2; i >= 0; --i) {
            maxHeapify(a, i, heapSize);
        } 
    }

    public void maxHeapify(int[] a, int i, int heapSize) {
        int l = i * 2 + 1, r = i * 2 + 2, largest = i;
        if (l < heapSize && a[l] > a[largest]) {
            largest = l;
        } 
        if (r < heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            swap(a, i, largest);
            maxHeapify(a, largest, heapSize);
        }
    }

    public void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}