剑指 Offer II 071. 按权重生成随机数（528. 按权重随机选择）

题目：

 

 

 

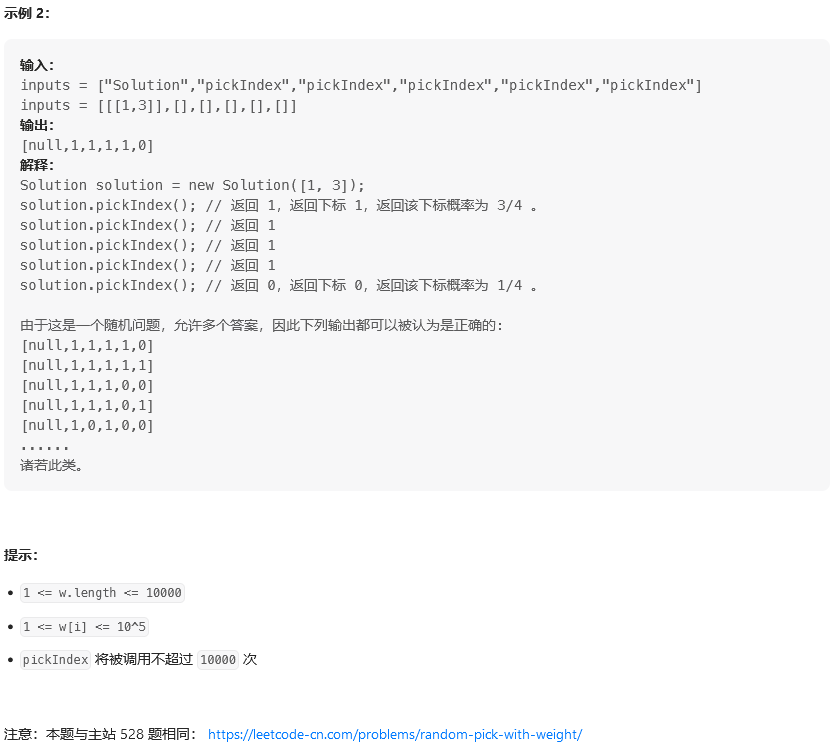
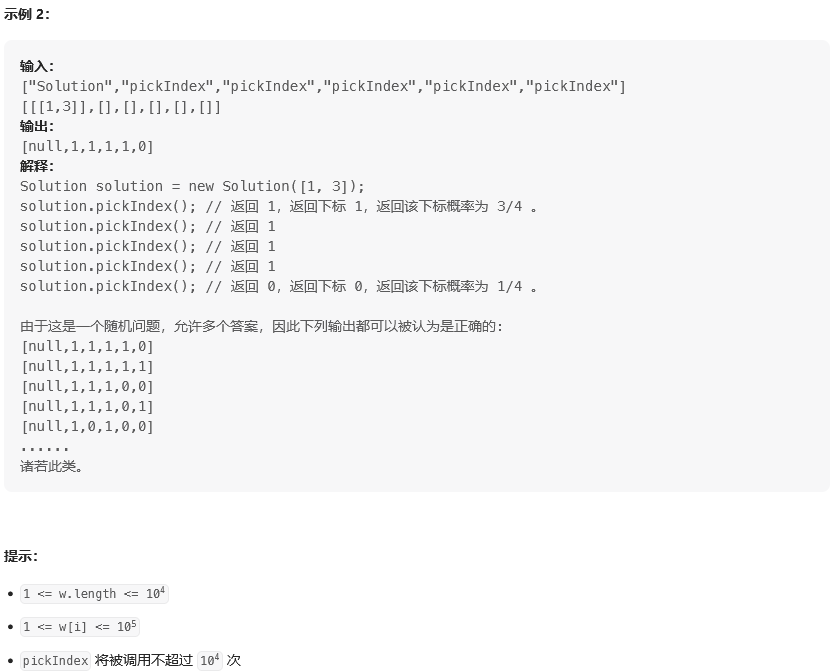
思路：

【1】其实如果是考虑最快取出来的话，应该是对于在数组中填充对应个数的下标，如【1,3】那么对应存储的数组应该是【0,1,1,1】，这种通过随机数获取下标是最快能拿出来的，但是弊端也很明显，需要的空间很大，就如【100,500,1】，这种如果导致内存溢出。所以需要换种方式。

【2】前缀和 + 二分查找：前缀和是参考了范围值的思想，如100，那么0-100的范围归属于0,而后的500，则是100-600的范围归属于1，这种算是用了最少的内存表达了区间。而后又要知道随机值在哪个区间，最快的便是二分查找了。

代码展示：

//时间25 ms击败59.13%
//内存45.9 MB击败59.41%
//时间复杂度：初始化的时间复杂度为 O(n)，每次选择的时间复杂度为 O(log⁡n)，其中 n 是数组 w 的长度。
//空间复杂度：O(n)，即为前缀和数组 pre 需要使用的空间。
class Solution {
    int[] pre;
    int total;
    
    public Solution(int[] w) {
        pre = new int[w.length];
        pre[0] = w[0];
        for (int i = 1; i < w.length; ++i) {
            pre[i] = pre[i - 1] + w[i];
        }
        total = Arrays.stream(w).sum();
    }
    
    public int pickIndex() {
        int x = (int) (Math.random() * total) + 1;
        return binarySearch(x);
    }

    private int binarySearch(int x) {
        int low = 0, high = pre.length - 1;
        while (low < high) {
            int mid = (high - low) / 2 + low;
            if (pre[mid] < x) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }
        return low;
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(w);
 * int param_1 = obj.pickIndex();
 */


//时间21 ms击败100%
//内存46 MB击败44.25%
class Solution {
    // 讲这种每次都要生成的变为只生成一次，然后不断使用，这种优化大概算是参考单例模式
    // 不过这种最好应该是变为静态变量
    Random rd =  new Random();
    int sum = 0;
    int len ;
    int[] pre;
    public Solution(int[] w) {
        len = w.length;
        pre = new int[len];
        pre[0] = w[0];
        for(int i = 1; i< len ; i++){
            pre[i] = pre[i-1] + w[i];
        } 

        sum = pre[len-1];
        
    }
    
    public int pickIndex() {
        int item = rd.nextInt(sum) + 1;
        int l = 0, r = len;
        while(l < r){
            int mid = (l + r) >> 1;
            if(pre[mid] < item) l = mid + 1;
            else r = mid;
        }

        return l;
    }
}