剑指 Offer II 038. 每日温度（739. 每日温度）

题目：

 

 

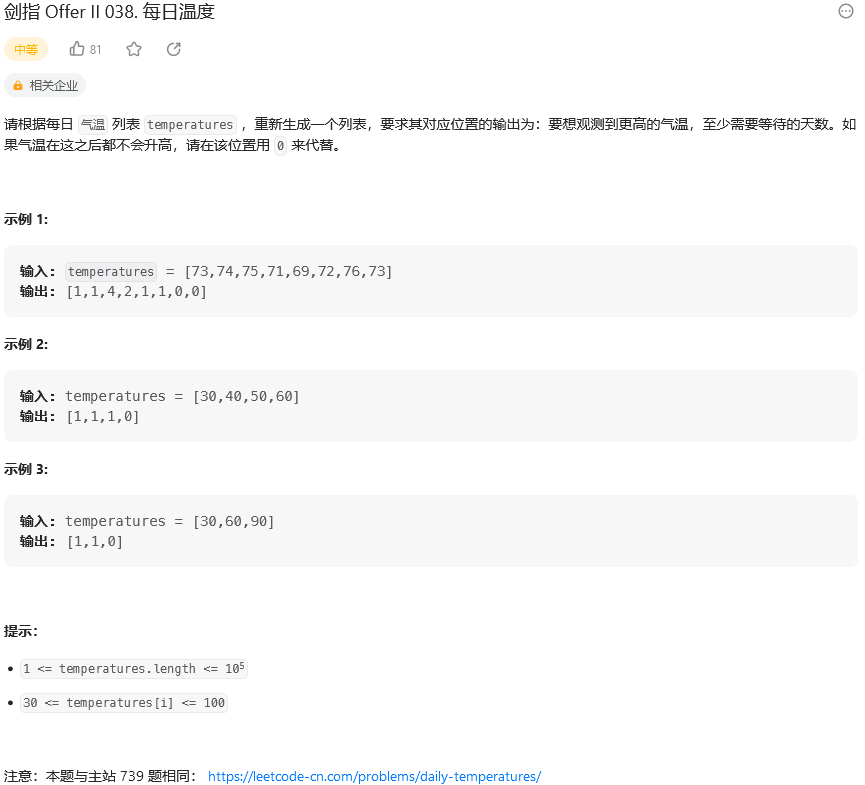
思路：

【1】利用最大队列的思想（参考 面试题59 - II. 队列的最大值 ）

【2】单调栈的思路（与上面利用队列最大值的思路差不多）：

原理分析：
对于温度列表 [73,74,75,71,69,72,76,73]，单调栈 stack 的初始状态为空，答案 ans 的初始状态是 [0,0,0,0,0,0,0,0]，
按照以下步骤更新单调栈和答案，其中单调栈内的元素都是下标，括号内的数字表示下标在温度列表中对应的温度。

    当 i=0 时，单调栈为空，因此将 0 进栈。
        stack=[0(73)]
        ans=[0,0,0,0,0,0,0,0]

    当 i=1 时，由于 74 大于 73，因此移除栈顶元素 0，赋值 ans[0]:=1−0，将 1 进栈。
        stack=[1(74)]
        ans=[1,0,0,0,0,0,0,0]

    当 i=2 时，由于 75 大于 74，因此移除栈顶元素 1，赋值 ans[1]:=2−1，将 2 进栈。
        stack=[2(75)]
        ans=[1,1,0,0,0,0,0,0]

    当 i=3 时，由于 71 小于 75，因此将 3 进栈。
        stack=[2(75),3(71)]
        ans=[1,1,0,0,0,0,0,0]

    当 i=4 时，由于 69 小于 71，因此将 4 进栈。
        stack=[2(75),3(71),4(69)]
        ans=[1,1,0,0,0,0,0,0]

    当 i=5 时，由于 72 大于 69 和 71，因此依次移除栈顶元素 4 和 3，赋值 ans[4]:=5−4 和 ans[3]:=5−3，将 5 进栈。
        stack=[2(75),5(72)]
        ans=[1,1,0,2,1,0,0,0]

    当 i=6 时，由于 76 大于 72 和 75，因此依次移除栈顶元素 5 和 2，赋值 ans[5]:=6−5 和 ans[2]:=6−2，将 6 进栈。
        stack=[6(76)]
        ans=[1,1,4,2,1,1,0,0]

    当 i=7 时，由于 73 小于 76，因此将 7 进栈。
        stack=[6(76),7(73)]
        ans=[1,1,4,2,1,1,0,0]

 

【3】暴力的方式

由于温度范围在 [30, 100] 之内，因此可以维护一个数组 next 记录每个温度第一次出现的下标。
数组 next 中的元素初始化为无穷大，在遍历温度列表的过程中更新 next 的值。

反向遍历温度列表。对于每个元素 temperatures[i]，
在数组 next 中找到从 temperatures[i] + 1 到 100 中每个温度第一次出现的下标，
将其中的最小下标记为 warmerIndex，则 warmerIndex 为下一次温度比当天高的下标。
如果 warmerIndex 不为无穷大，则 warmerIndex - i 即为下一次温度比当天高的等待天数，
最后令 next[temperatures[i]] = i。

 

代码展示：

暴力的方式：

//时间39 ms击败49.49%
//内存55 MB击败38.49%
//时间复杂度：O(nm)，其中 n 是温度列表的长度，m 是数组 next 的长度，在本题中温度不超过 100，所以 m 的值为 100。反向遍历温度列表一遍，对于温度列表中的每个值，都要遍历数组 next 一遍。
//空间复杂度：O(m)，其中 m 是数组 next 的长度。除了返回值以外，需要维护长度为 m 的数组 next 记录每个温度第一次出现的下标位置。
class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int length = temperatures.length;
        int[] ans = new int[length];
        int[] next = new int[101];
        Arrays.fill(next, Integer.MAX_VALUE);
        for (int i = length - 1; i >= 0; --i) {
            int warmerIndex = Integer.MAX_VALUE;
            for (int t = temperatures[i] + 1; t <= 100; ++t) {
                if (next[t] < warmerIndex) {
                    warmerIndex = next[t];
                }
            }
            if (warmerIndex < Integer.MAX_VALUE) {
                ans[i] = warmerIndex - i;
            }
            next[temperatures[i]] = i;
        }
        return ans;
    }
}

 

单调栈的思路：

//时间23 ms击败90.86%
//内存56.9 MB击败36.1%
//时间复杂度：O(n)，其中 n 是温度列表的长度。
//正向遍历温度列表一遍，对于温度列表中的每个下标，最多有一次进栈和出栈的操作。
//空间复杂度：O(n)，其中 n 是温度列表的长度。需要维护一个单调栈存储温度列表中的下标。
class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int length = temperatures.length;
        int[] ans = new int[length];
        Deque<Integer> stack = new LinkedList<Integer>();
        for (int i = 0; i < length; i++) {
            int temperature = temperatures[i];
            while (!stack.isEmpty() && temperature > temperatures[stack.peek()]) {
                int prevIndex = stack.pop();
                ans[prevIndex] = i - prevIndex;
            }
            stack.push(i);
        }
        return ans;
    }
}

 

利用最大队列的思想：

//时间38 ms击败45.58%
//内存57.1 MB击败29.11%
class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        //以{73,74,75,71,69,72,76,73}为例
        int[] res = new int[temperatures.length];
        LinkedList<Integer> queue = new LinkedList<>();
        queue.addFirst(temperatures.length-1);
        for (int i = temperatures.length-2; i >= 0; i--){
            int index = 0;
            //利用队列的特性，当现在为71时，此时队列内有【69,72,76】,因为69小所以下移到另一个
            while (index < queue.size() && temperatures[i] >= temperatures[queue.get(index)]) index++;
            //这里保证了右边存在比当前数要大的才会记录，小的直接跳过
            if (index < queue.size()) res[i] = queue.get(index) - i;
            //当现在为71时，此时队列内有【69,72,76】，因为71大于69，所以比71大的必然比69大，所以69用不到了应该移除
            while (!queue.isEmpty() && temperatures[i] >= temperatures[queue.peekFirst()]) queue.pollFirst();
            //添加后队列为【71,72,76】
            queue.addFirst(i);
        }
        return res;
    }
}