剑指 Offer II 099. 最小路径之和（64. 最小路径和）

题目：

 

 

 

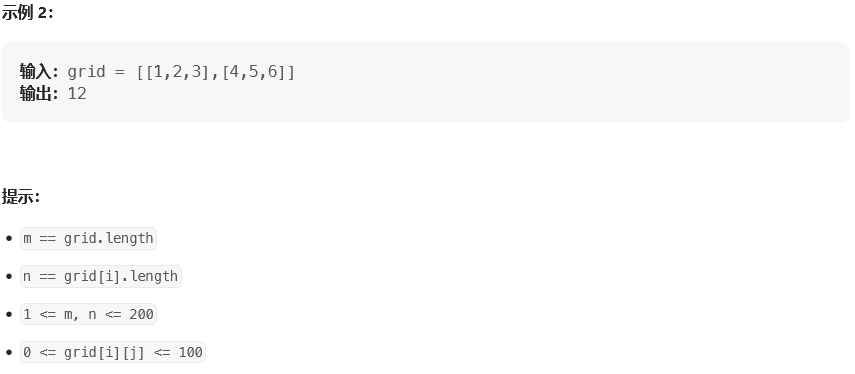
思路：

【1】动态规划的方式

【2】使用深度优先的方式

代码展示：

动态规划的方式：

//时间2 ms击败94.62%
//内存44 MB击败53.97%
//时间复杂度：O(mn)，其中 m 和 n 分别是网格的行数和列数。需要对整个网格遍历一次，计算 dp 的每个元素的值。
//空间复杂度：O(mn)，其中 m 和 n 分别是网格的行数和列数。创建一个二维数组 dp，和网格大小相同。
//空间复杂度可以优化，例如每次只存储上一行的 dp 值，则可以将空间复杂度优化到 O(n)。
//标准的动态规划的方式
class Solution {
    public int minPathSum(int[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {
            return 0;
        }
        int rows = grid.length, columns = grid[0].length;
        int[][] dp = new int[rows][columns];
        dp[0][0] = grid[0][0];
        for (int i = 1; i < rows; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < columns; j++) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < rows; i++) {
            for (int j = 1; j < columns; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[rows - 1][columns - 1];
    }
}

//当然代码量是可以减少的
//时间2 ms击败94.62%
//内存44 MB击败56.18%
//空间复杂度直接为O(1)了，因为当走到某一位置的时候直接将达到该位置的所花费最小的代价加上该位置本身的数值
//最重要的是你只能往下和往右走，所以固定了该位置来上一个位置的方向
class Solution {
    public int minPathSum(int[][] grid) {
        for(int i = 1;i < grid.length;i++) grid[i][0] += grid[i-1][0];
      
        for(int i = 1;i < grid[0].length;i++) grid[0][i] += grid[0][i-1];
   
        for(int i = 1;i < grid.length;i++) {
            for(int j = 1;j < grid[0].length;j++) {
                grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);
            }
        }
        return grid[grid.length-1][grid[0].length-1];
    }
}