剑指 Offer II 092. 翻转字符（926. 将字符串翻转到单调递增）

题目：

 

 

 

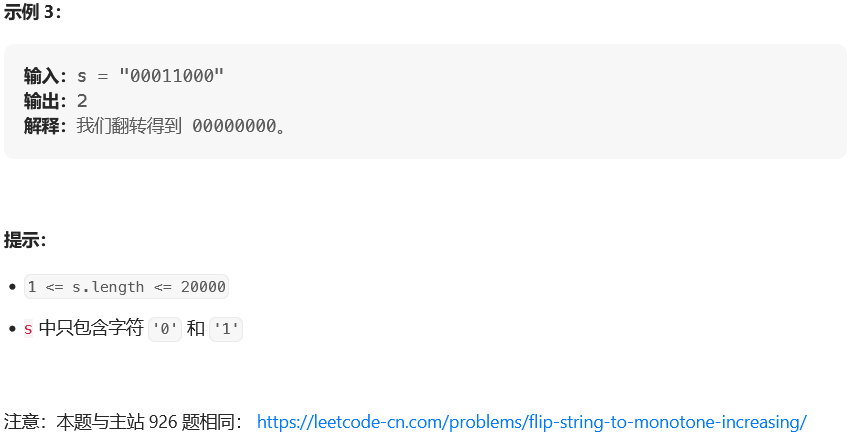
思路：

【1】动态规划的方式

【2】前缀和的方式

代码展示：

前缀和的方式：

//时间16 ms击败36.61%
//内存42.2 MB击败47.49%
//本身就是利用了：最终的字符串左边全 0 右边全1的特性
//（假设到了某个点，该点不反转，将左边的全部置为0，与右边全部置为1）
//（通过全部列举的到全部答案，然后从中找出翻转最少的）
//时间复杂度：O(n)
//空间复杂度：O(n)
//思路比较清晰的版本
class Solution {
    public int minFlipsMonoIncr(String s) {
        char[] c = s.toCharArray();
        int length = c.length;

        int[] left = new int[length];
        int[] right = new int[length];
        for (int i = 1; i < length; i++) {
            left[i] += left[i - 1];
            if (c[i - 1] == '1') left[i]++;
        }

        for (int i = length - 2; i >= 0; i--) {
            right[i] += right[i + 1];
            if (c[i + 1] == '0')  right[i]++;
        }
        
        int res = length;
        for (int i = 0; i < length; i++) {
            res = Math.min(left[i] + right[i], res);
        }
        return res;
    }
}

//优化的版本
//时间6 ms击败98.54%
//内存42.1 MB击败56.28%
class Solution {
    public int minFlipsMonoIncr(String s) {
        char[] cs = s.toCharArray();
        int n = cs.length, ans = n;
        int[] sum = new int[n + 10];
        for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + (cs[i - 1] - '0');
        for (int i = 1; i <= n; i++) {
            int l = sum[i - 1], r = (n - i) - (sum[n] - sum[i]);
            ans = Math.min(ans, l + r);
        }
        return ans;
    }
}

 

动态规划的方式：

//时间41 ms击败7.95%
//内存49.5 MB击败9.63%
//规范的动态规划写法
class Solution {
    //dp[i][0]表示前i个元素，最后一个元素为0的最小翻转次数；
    //dp[i][1]表示前i个元素，最后一个元素为1的最小翻转次数
    public int minFlipsMonoIncr(String s) {
        int dp[][]=new int[s.length()][2];
        // 初始化
        // 这里分明是列举了两种情况，dp[0][0]代表最后元素为0的情况，dp[0][1]代表最后元素为1的情况
        // 其次为什么是要记录两个呢？因为字符 0 前面的相邻字符一定是 0，字符 1 前面的相邻字符可以是 0 或 1。
        dp[0][0]=s.charAt(0)=='0'?0:1;
        dp[0][1]=s.charAt(0)=='1'?0:1;
        //状态转移
        for (int i = 1; i <s.length() ; i++) {
            dp[i][0]=dp[i-1][0]+(s.charAt(i)=='0'?0:1);
            dp[i][1]=Math.min(dp[i-1][0],dp[i-1][1])+(s.charAt(i)=='1'?0:1);
        }
        return Math.min(dp[s.length()-1][0],dp[s.length()-1][1]);
    }
}

//又由于使用动态规划的话，其实不一定需要保留那么多变量，所以存储的变量可以简化
//时间4 ms击败99.37%
//内存42 MB击败70.92%
//时间复杂度：O(n)，其中 n 是字符串 s 的长度。需要遍历字符串一次，对于每个字符计算最小翻转次数的时间都是 O(1)。
//空间复杂度：O(1)。使用空间优化的方法，空间复杂度是 O(1)
class Solution {
    public int minFlipsMonoIncr(String s) {
        int dp0 = 0, dp1 = 0;
        for (char ch : s.toCharArray()) {
            //先更新dp[i][1]，需要用到dp[i-1][0] 由于只有0和1，也不在使用三目运算
            dp1 = Math.min(dp0, dp1) + ('1' - ch);
            dp0 += ch - '0';
        }
        return Math.min(dp0, dp1);
    }
}