剑指 Offer II 118. 多余的边（684. 冗余连接）

题目：

 

 

 

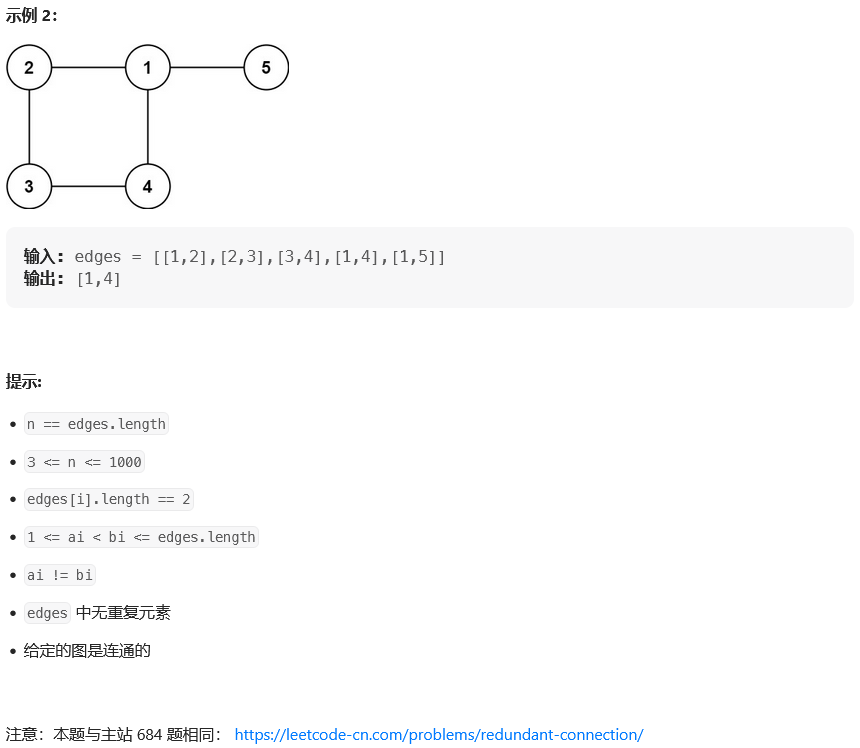
思路：

【1】并查集

代码展示：

//时间0 ms击败100%
//内存41.4 MB击败90.40%
//时间复杂度：O(nlog⁡n)，其中 n 是图中的节点个数。
//需要遍历图中的 n 条边，对于每条边，需要对两个节点查找祖先，如果两个节点的祖先不同则需要进行合并，需要进行 2 次查找和最多 1 次合并。
//一共需要进行 2n 次查找和最多 n 次合并，因此总时间复杂度是 O(2n*log⁡n)=O(nlog⁡n)。
//这里的并查集使用了路径压缩，但是没有使用按秩合并，最坏情况下的时间复杂度是 O(nlog⁡n)，平均情况下的时间复杂度依然是 O(nα(n))，其中 α 为阿克曼函数的反函数，α(n) 可以认为是一个很小的常数。
//空间复杂度：O(n)，其中 n 是图中的节点个数。使用数组 parent 记录每个节点的祖先。
class Solution {
    //以edges = new int[][]{{1,2}, {2,3}, {3,4}, {1,4}, {1,5}};为例
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        //记录每条边的父节点
        int[] parent = new int[n + 1];
        //先是设定父节点为自身，初始化每个节点的父节点：[0, 1, 2, 3, 4, 5]
        for (int i = 1; i <= n; i++) {
            parent[i] = i;
        }
        for (int i = 0; i < n; i++) {
            int[] edge = edges[i];
            int node1 = edge[0], node2 = edge[1];
            //例子1，以{1,2}为例
            if (find(parent, node1) != find(parent, node2)) {
                //对两个节点进行合并
                union(parent, node1, node2);
            } else {
                return edge;
            }
        }
        return new int[0];
    }
    //传入parent和1和2，合并之后的父节点显示：[0, 2, 2, 3, 4, 5]
    public void union(int[] parent, int index1, int index2) {
        parent[find(parent, index1)] = find(parent, index2);
    }
    //传入parent和1
    //传入parent和2
    public int find(int[] parent, int index) {
        if (parent[index] != index) {
            parent[index] = find(parent, parent[index]);
        }
        return parent[index];
    }
}