剑指 Offer II 028. 展平多级双向链表（430. 扁平化多级双向链表）

题目：

 

 

 

 

 

 

 

 

 

 

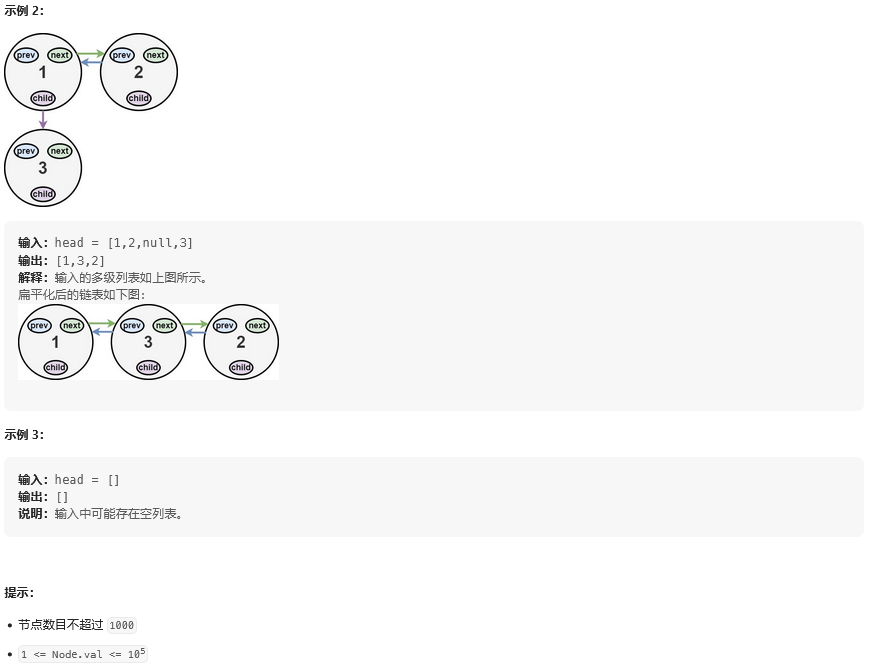
思路：

【1】利用递归的方式：

【2】利用遍历迭代的方式：

代码展示：

利用遍历迭代的方式：

// 1）使用辅助空间 ，使用辅助空间的目的是为了当遇到存在分支路线的时候，将主支的下一个节点保留
// 方便等分支处理完了后还能回到主支。
//时间0 ms击败100%
//内存39.4 MB击败83.13%
class Solution {
    public Node flatten(Node head) {
        Node node = head;
        Node prev = null;
        Deque<Node> stack = new ArrayDeque<>();
        while (node != null || !stack.isEmpty()) {
            if (node == null) {
                node = stack.pop();
                node.prev = prev;
                prev.next = node;
            }
            if (node.child != null) {
                if (node.next != null) stack.push(node.next);
                node.child.prev = node;
                node.next = node.child;
                node.child = null;
            }
            prev = node;
            node = node.next;
        }
        return head;
    }
}

// 2）不使用辅助空间 ，不使用辅助空间的原理是在原本的链表上进行了修改，将分支全部提到了主支上
// 如主支原本为AB,A下面存在分支CDE，那么提上来后变为A[CDE]B，这个过程CDE也会被当做是主支的成为纳入逻辑，
// 因为CDE也有可能存在分支
//时间0 ms击败100%
//内存39.6 MB击败52.95%
class Solution {
    public Node flatten(Node head) {
        Node dummy = new Node(0);
        dummy.next = head;
        for (; head != null; head = head.next) {
            if (head.child != null) {
                Node tmp = head.next;
                Node child = head.child;
                head.next = child;
                child.prev = head;
                head.child = null;
                Node last = head;
                while (last.next != null) last = last.next;
                last.next = tmp;
                if (tmp != null) tmp.prev = last;
            }
        }
        return dummy.next;
    }

}

 

利用递归的方式：

//时间0 ms击败100%
//内存39.5 MB击败63.17%
//时间复杂度：O(n)，其中 n 是链表中的节点个数。
//空间复杂度：O(n)。
//代码中使用的空间为深度优先搜索中的栈空间，如果给定的链表的「深度」为 d，那么空间复杂度为 O(d)。
//在最坏情况下，链表中的每个节点的 next 都为空，且除了最后一个节点外，每个节点的 child 都不为空，整个链表的深度为 n，因此时间复杂度为 O(n)。
/* // Definition for a Node.
class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
}; */
class Solution {
    public Node flatten(Node head) {
        dfs(head);
        return head;
    }

    public Node dfs(Node node) {
        Node cur = node;
        // 记录链表的最后一个节点
        Node last = null;

        while (cur != null) {
            Node next = cur.next;
            //  如果有子节点，那么首先处理子节点
            if (cur.child != null) {
                Node childLast = dfs(cur.child);

                next = cur.next;
                //  将 node 与 child 相连
                cur.next = cur.child;
                cur.child.prev = cur;

                //  如果 next 不为空，就将 last 与 next 相连
                if (next != null) {
                    childLast.next = next;
                    next.prev = childLast;
                }

                // 将 child 置为空
                cur.child = null;
                last = childLast;
            } else {
                last = cur;
            }
            cur = next;
        }
        return last;
    }
}