剑指 Offer II 013. 二维子矩阵的和（304. 二维区域和检索 - 矩阵不可变）

题目：

 

 

 

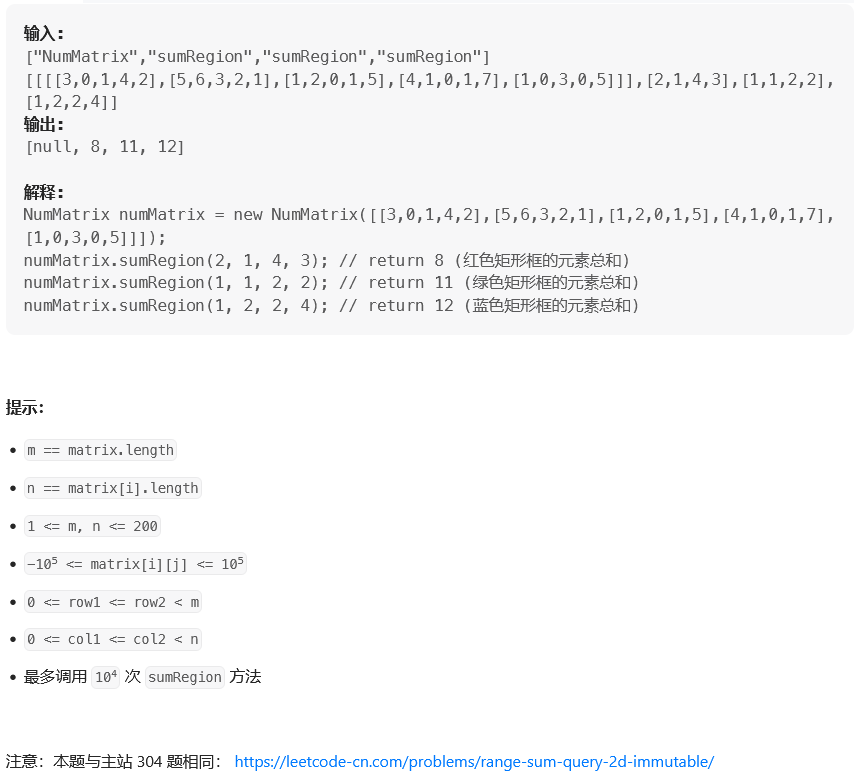
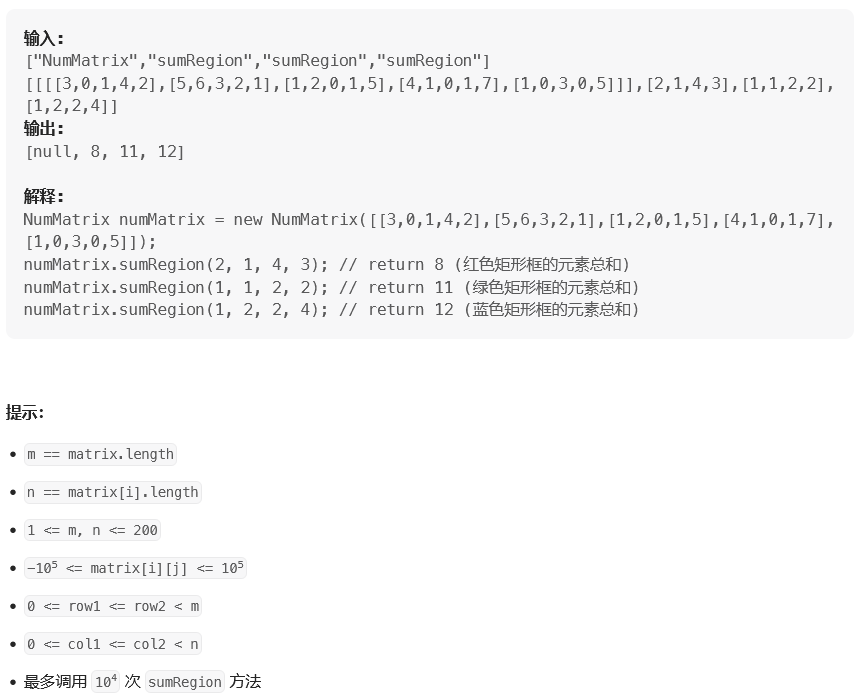
思路：

【1】基于暴力的思想

【2】基于数据集的思想（基于 303. 区域和检索 - 数组不可变 这道题）

代码展示：

基于暴力的思想（这种是不进行初始化，而是用到了就进行遍历，虽然节约空间（也不是很大），但是如果次数多，就会发现需要的时间是基于数据集思想的数十乃至上百倍）：

//时间1418 ms击败5.5%
//内存62.2 MB击败88.57%
class NumMatrix {
    private int[][] matrix;

    public NumMatrix(int[][] matrix) {
        this.matrix = matrix;
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; i++) {
            for (int j = col1; j <= col2; j++) {
                sum += matrix[i][j];
            }
        }
        return sum;
    }
}

基于数据集的思想（这种虽然借鉴了思想，但是转换成的数据集不完整，因为还是需要遍历拿出数据进行汇总，虽然比暴力思想要少很多，但是还是太多无用功，是不是可以仅一次计算就拿出结果这种呢）：

//时间136 ms击败11.87%
//内存64.9 MB击败29.61%
class NumMatrix {
    int[][] sums;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        if (m > 0) {
            int n = matrix[0].length;
            sums = new int[m][n + 1];
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sums[i][j + 1] = sums[i][j] + matrix[i][j];
                }
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; i++) {
            sum += sums[i][col2 + 1] - sums[i][col1];
        }
        return sum;
    }
}

 

数据集的优化（本质上是采用了空间换时间的方式，如果这种是执行次数多的话，就减少了遍历的次数，单一次计算就拿出了结果）：

//时间43 ms击败95.28%
//内存65.9 MB击败50.44%
//时间复杂度：初始化 O(mn)，每次检索 O(1)，其中 m 和 n 分别是矩阵 matrix 的行数和列数。 初始化需要遍历矩阵 matrix 计算二维前缀和，时间复杂度是 O(mn)。 每次检索的时间复杂度是 O(1)。
//空间复杂度：O(mn)，其中 m 和 n 分别是矩阵 matrix 的行数和列数。需要创建一个 m+1 行 n+1 列的二维前缀和数组 sums。
class NumMatrix {
    int[][] sums;
    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        if (m > 0) {
            int n = matrix[0].length;
            sums = new int[m + 1][n + 1];
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];
                }
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */