剑指 Offer II 088. 爬楼梯的最少成本（746. 使用最小花费爬楼梯）

题目：

 

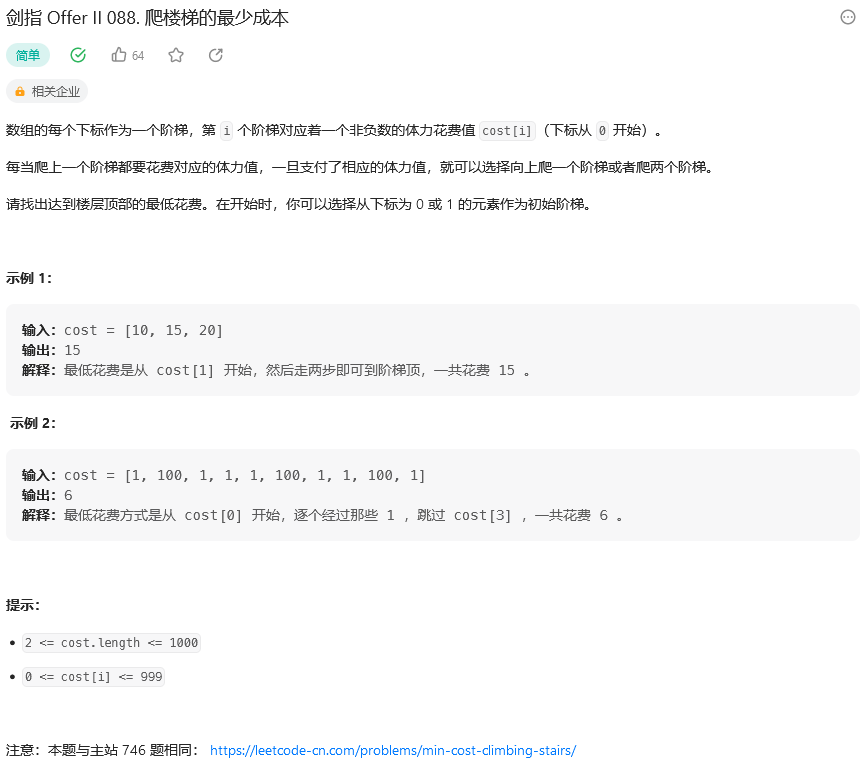
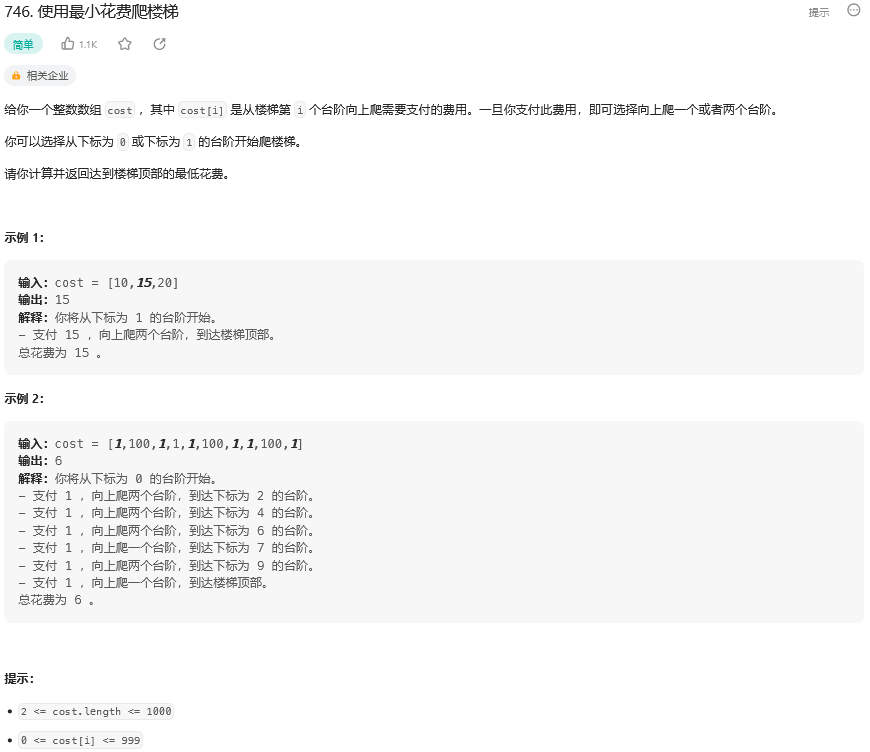
思路：

【1】个人理解：

体力值  10  15  20    
水平线   0   1   2  天台
1.也就是说天台其实算是数组溢出一位来着。
2.可以选择0或者1位索引的阶梯为初始阶梯
3.一次最多可以跨两步，而且花费的体力为离开该位置的体力，如无论从0到1，还是从0到2，所花费的体力都是arr【0】

 

【2】模拟的方式

因为本质上是要选取消耗体力最小的
那么其实算是跳台阶的变种
假设要跳到第N个台阶，那么必然是要从N-1或者N-2的地方起跳
故得出F(N) = Math.min(F(N-1),F(N-2))

 

【3】动态规划

代码展示：

动态规划的方式：

//时间0 ms击败100%
//内存41.3 MB击败20.81%
//时间复杂度和空间复杂度都是 O(n)
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int[] dp = new int[n + 1];
        dp[0] = dp[1] = 0;
        for (int i = 2; i <= n; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[n];
    }
}

//因为其实只用到了两个结果，所以可以对空间再进行优化
//时间0 ms击败100%
//内存41 MB击败61.14%
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int prev = 0, curr = 0;
        for (int i = 2; i <= n; i++) {
            int next = Math.min(curr + cost[i - 1], prev + cost[i - 2]);
            prev = curr;
            curr = next;
        }
        return curr;
    }
}

 

模拟的方式：

//时间0 ms击败100%
//内存40.9 MB击败82.38%
//相当于将原本的数组空间作为了动态规划的放置
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int len = cost.length;
        for(int i = 2; i < len; i ++){
            cost[i] += Math.min(cost[i - 1], cost[i - 2]);
        }
        return Math.min(cost[len - 1], cost[len - 2]);
    }
}