剑指 Offer 51. 数组中的逆序对

题目：

思路：

【1】暴力是比较容易超时的，然后我有考虑使用堆排序，貌似不太行，排完序，还是需要多次遍历。

【2】使用归并算法

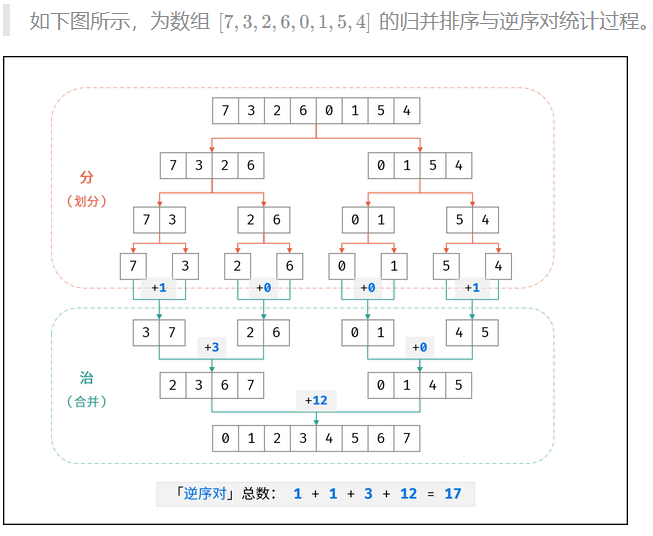
代码展示：

基于归并排序的方式：

//时间35 ms击败25.1%
//内存49 MB击败71.27%
//时间复杂度：同归并排序 O(nlog⁡n)。
//空间复杂度：同归并排序 O(n)，因为归并排序需要用到一个临时数组。
class Solution {
    int[] nums, tmp;

    public int reversePairs(int[] nums) {
        this.nums = nums;
        tmp = new int[nums.length];
        return mergeSort(0, nums.length - 1);
    }

    private int mergeSort(int l, int r) {

        // 终止条件
        if (l >= r) return 0;

        // 递归划分
        int m = (l + r) / 2;
        int res = mergeSort(l, m) + mergeSort(m + 1, r);

        // 合并阶段
        int i = l, j = m + 1;
        for (int k = l; k <= r; k++)
            tmp[k] = nums[k];

        for (int k = l; k <= r; k++) {
            if (i == m + 1)
                nums[k] = tmp[j++];
            else if (j == r + 1 || tmp[i] <= tmp[j])
                nums[k] = tmp[i++];
            else {
                nums[k] = tmp[j++];
                res += m - i + 1; // 统计逆序对
            }
        }
        return res;
    }
}

优化的写法（本质思路是一样的，但是耗费的时间的话下面的更少）：

//时间29 ms击败89.36%
//内存49.1 MB击败59.30%
class Solution {
    public int mergeAndCount(int[] nums,int[] temp,int left,int mid,int right){
        int i=left;
        int j=mid+1;
        int k=left;
        int count=0;
        while(i<=mid&&j<=right){
            if(nums[i]<=nums[j]){
                temp[k++]=nums[i++];
            }else{
                temp[k++]=nums[j++];
                count+=(mid+1-i);
            }
        }
        while(i<=mid){
            temp[k++]=nums[i++];
        }
        while(j<=right){
            temp[k++]=nums[j++];
        }
        for(i=left;i<=right;i++){
            nums[i]=temp[i];
        }
        return count;

    }
    public int mergeSort(int[] nums,int[] temp,int left,int right){
        if(left>=right){
            return 0;
        }
        int mid=left+(right-left)/2;
        int leftCount=mergeSort(nums,temp,left,mid);
        int rightCount=mergeSort(nums,temp,mid+1,right);
        if(nums[mid]<=nums[mid+1]){
            return leftCount+rightCount;
        }
        int crossCount=mergeAndCount(nums,temp,left,mid,right);
        return leftCount+crossCount+rightCount;

    }
    public int reversePairs(int[] nums) {
        if(nums.length<2) return 0;
        int[] temp=new int[nums.length];
        return mergeSort(nums,temp,0,nums.length-1);
    }
}

 

暴力破解的方式（结果显然是会超出时间限制，毕竟时间复杂度O(N^2)）：

class Solution {
    public int reversePairs(int[] nums) {
        int count = 0;
        for (int i = 0; i < nums.length-1; i++){
            for (int j = i+1; j < nums.length; j++){
                if (nums[i] > nums[j]) count++;
            }
        }
        return count;
    }
}