剑指 Offer 59 - I. 滑动窗口的最大值（239. 滑动窗口最大值）

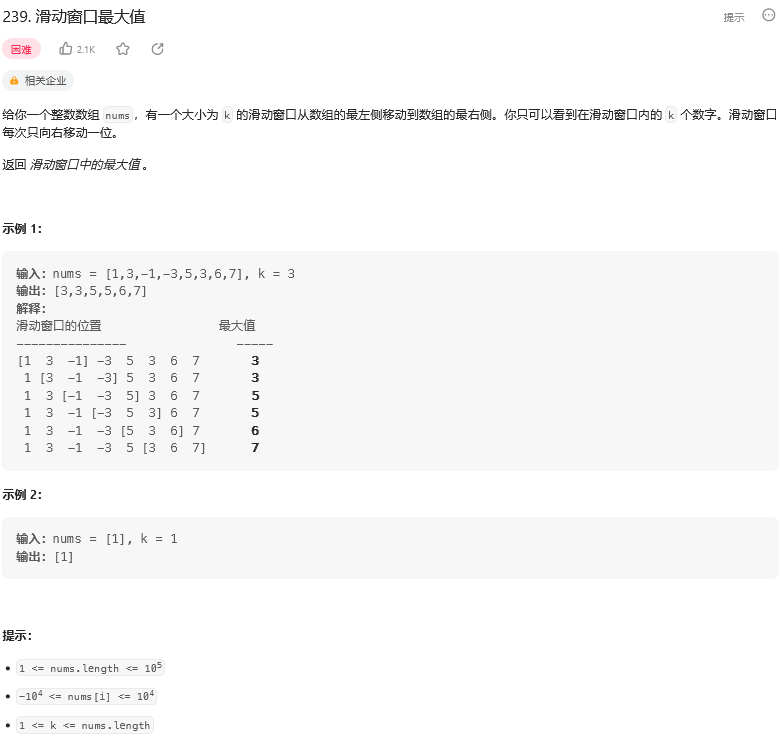
题目：

 

 

 

思路：

【1】看到这里，我首先想到的是使用队列来完成，因为用一个辅助空间存储最大值即可，思路可以参考  面试题59 - II. 队列的最大值  。里面内容很相似，问如果每次往对里面添加数据，然后可以通过某个函数获取到里面的最大值。当然有用双循环的方式其实是都可以做的，但是这样耗时会更大，因为需要多次遍历，而且随着数据量的增大，会成指数性的上升。

【2】其次基于最大最小的问题，一般我们都会考虑使用堆，那么也就是使用优先队列来完成。但是这种的需要的内存相对会大很多，而且也会带来耗时增加，因为不是只做记录而是存储很多需要遍历的东西。

代码展示：

使用优先队列的方式：

//时间88 ms击败9.15%
//内存58.3 MB击败45.11%
//时间复杂度：O(nlog⁡n)，其中 n 是数组 nums 的长度。在最坏情况下，数组 nums 中的元素单调递增，那么最终优先队列中包含了所有元素，没有元素被移除。
//由于将一个元素放入优先队列的时间复杂度为 O(log⁡n)，因此总时间复杂度为 O(nlog⁡n)。
//空间复杂度：O(n)，即为优先队列需要使用的空间。
//这里所有的空间复杂度分析都不考虑返回的答案需要的 O(n)空间，只计算额外的空间使用。
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || nums.length == 0) return new int[]{};
        int n = nums.length;
        //转为lamdba表达式
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>((pair1, pair2) -> pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1]);
        //lamdba表达式转换前的写法
//        PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
//            public int compare(int[] pair1, int[] pair2) {
//                return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
//            }
//        });
        for (int i = 0; i < k; ++i) {
            pq.offer(new int[]{nums[i], i});
        }
        int[] ans = new int[n - k + 1];
        ans[0] = pq.peek()[0];
        for (int i = k; i < n; ++i) {
            pq.offer(new int[]{nums[i], i});
            while (pq.peek()[1] <= i - k) {
                pq.poll();
            }
            ans[i - k + 1] = pq.peek()[0];
        }
        return ans;
    }
}

 

单调队列的方式：

//时间26 ms击败93.12%
//内存57.5 MB击败67.81%
//时间复杂度：O(n)，其中 n 是数组 nums 的长度。
//每一个下标恰好被放入队列一次，并且最多被弹出队列一次，因此时间复杂度为 O(n)。
//空间复杂度：O(k)。不断从队首弹出元素的条件，保证了队列中最多不会有超过 k+1 个元素，因此队列使用的空间为 O(k)。
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || nums.length == 0) return new int[]{};
        //基于k<nums.length
        int[] res = new int[nums.length-k+1];
        LinkedList<Integer> maxQueue = new LinkedList<Integer>();
        for (int i = 0; i < k; i++){
            //要知道这里是从队列的右边出
            //如之前已经【9，5，4，3】那么当6加入的时候其实，当9弹出后，这组数据的最大值应该是6，所以5,4,3都应该被清理
            while (!maxQueue.isEmpty() && nums[maxQueue.peekLast()] <= nums[i]) {
                maxQueue.pollLast();
            }
            maxQueue.add(i);
        }
        //这里使用peek()或者peekFirst()都一样，方法内代码都一样
        res[0] = nums[maxQueue.peek()];
        //那么剩下的就要像之前一样先加入到队列
        //然后判断是不是队列的元素已经到了边界需要弹出
        for (int i = k; i < nums.length; i++) {
            while (!maxQueue.isEmpty() && nums[i] >= nums[maxQueue.peekLast()]) {
                maxQueue.pollLast();
            }
            maxQueue.offerLast(i);
            while (maxQueue.peek() <= i - k) {
                //这里使用poll()或者pollFirst()都一样，方法内代码都一样
                maxQueue.poll();
            }
            res[i - k + 1] = nums[maxQueue.peek()];
        }

        return res;
    }
}

暴力双循环的方式（超出时间限制）：

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || nums.length == 0) return new int[]{};
        int[] res = new int[nums.length-k+1];
        int max;
        for (int i = 0; i < nums.length - k + 1; i++){
            max = Integer.MIN_VALUE;
            for (int j = i; j < i+k ; j++){
                max = Math.max(max,nums[j]);
            }
            res[i] = max;
        }
        return res;
    }
}