剑指 Offer 68 - II. 二叉树的最近公共祖先(236. 二叉树的最近公共祖先)
题目:
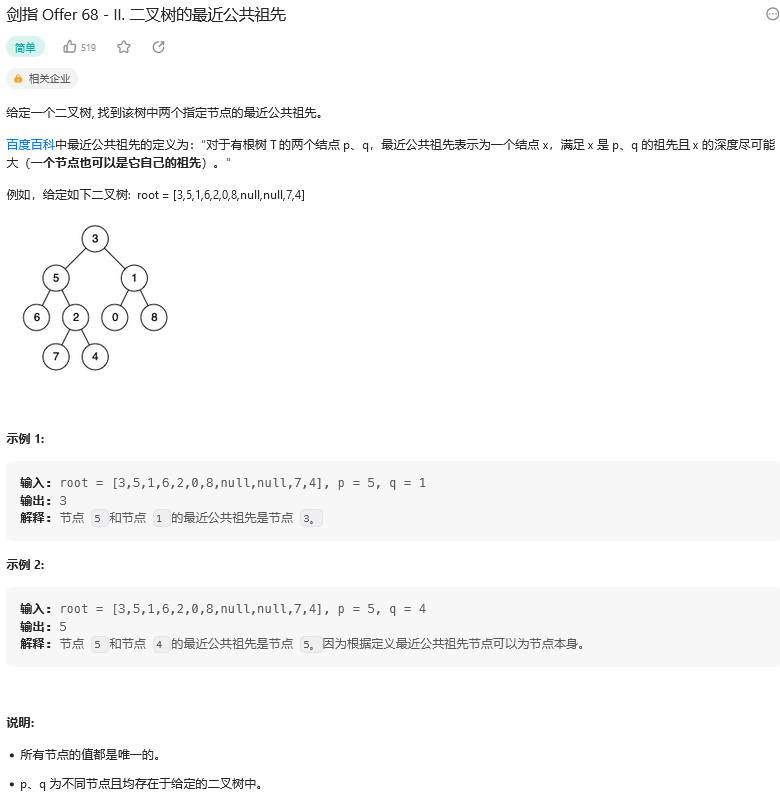
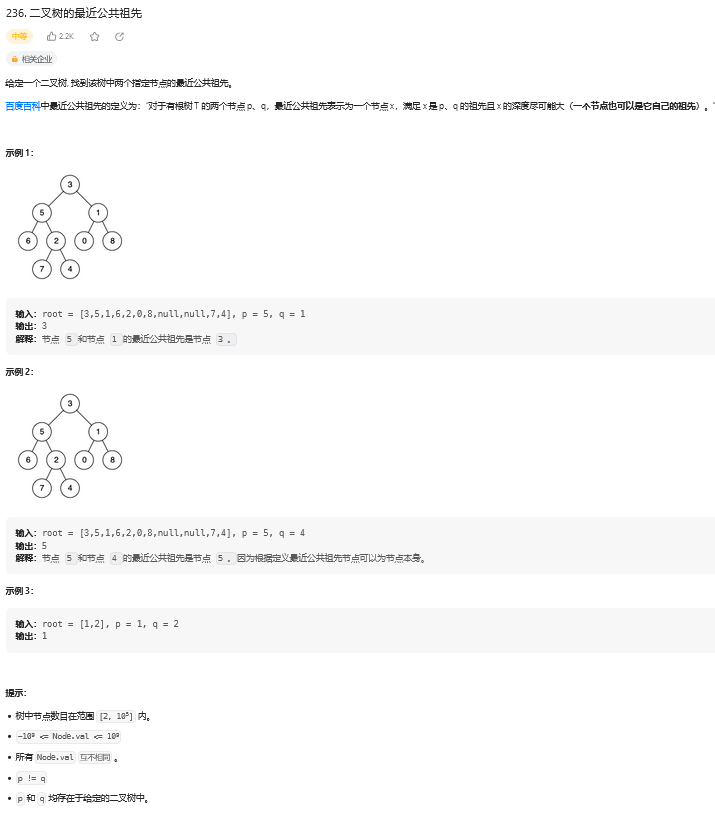
思路:
【1】简单暴力的方式就是全遍历,使用辅助空间Map记录所有节点的,然后根据其中一个节点,将其链条内的节点【即从根目录】都塞入Set中,然后第二个节点也如一样的方式,当第一个出现的共同父节点既是公共先祖。
【2】使用递归的方式:可以判断出根据两个子节点的返回值
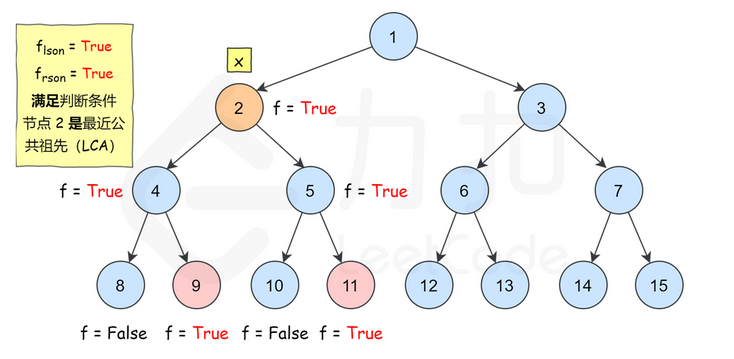
【3】构建示例代码:
构建示例代码: class TreeNode { int val; TreeNode left; TreeNode right; TreeNode() {} TreeNode(int val) { this.val = val; } TreeNode(int val, TreeNode left, TreeNode right) { this.val = val; this.left = left; this.right = right; } @Override public String toString() { return "TreeNode{" + "val=" + val + ", left=" + left + ", right=" + right + '}'; } } public static TreeNode l; public static TreeNode r; public static TreeNode getTestTree(){ TreeNode Node1 = new TreeNode(1); TreeNode Node2 = new TreeNode(2); TreeNode Node3 = new TreeNode(3); Node1.left = Node2; Node1.right = Node3; TreeNode Node4 = new TreeNode(4); TreeNode Node5 = new TreeNode(5); Node2.left = Node4; Node2.right = Node5; TreeNode Node6 = new TreeNode(6); TreeNode Node7 = new TreeNode(7); Node3.left = Node6; Node3.right = Node7; TreeNode Node8 = new TreeNode(8); TreeNode Node9 = new TreeNode(9); Node4.left = Node8; Node4.right = Node9; TreeNode Node10 = new TreeNode(10); TreeNode Node11 = new TreeNode(11); Node5.left = Node10; Node5.right = Node11; TreeNode Node12 = new TreeNode(12); TreeNode Node13 = new TreeNode(13); Node6.left = Node12; Node6.right = Node13; TreeNode Node14 = new TreeNode(14); TreeNode Node15 = new TreeNode(15); Node7.left = Node14; Node7.right = Node15; l = Node9; r = Node11; return Node1; }
【4】大致结果流程:
每个节点的输出 TreeNode{val=8, left=null, right=null} L:null R:null 每个节点的输出 TreeNode{val=4, left=TreeNode{val=8, left=null, right=null}, right=TreeNode{val=9, left=null, right=null}} L:null R:TreeNode{val=9, left=null, right=null} 每个节点的输出 TreeNode{val=10, left=null, right=null} L:null R:null 每个节点的输出 TreeNode{val=5, left=TreeNode{val=10, left=null, right=null}, right=TreeNode{val=11, left=null, right=null}} L:null R:TreeNode{val=11, left=null, right=null} 每个节点的输出 TreeNode{val=2, left=TreeNode{val=4, left=TreeNode{val=8, left=null, right=null}, right=TreeNode{val=9, left=null, right=null}}, right=TreeNode{val=5, left=TreeNode{val=10, left=null, right=null}, right=TreeNode{val=11, left=null, right=null}}} L:TreeNode{val=9, left=null, right=null} R:TreeNode{val=11, left=null, right=null} 每个节点的输出 TreeNode{val=12, left=null, right=null} L:null R:null 每个节点的输出 TreeNode{val=13, left=null, right=null} L:null R:null 每个节点的输出 TreeNode{val=6, left=TreeNode{val=12, left=null, right=null}, right=TreeNode{val=13, left=null, right=null}} L:null R:null 每个节点的输出 TreeNode{val=14, left=null, right=null} L:null R:null 每个节点的输出 TreeNode{val=15, left=null, right=null} L:null R:null 每个节点的输出 TreeNode{val=7, left=TreeNode{val=14, left=null, right=null}, right=TreeNode{val=15, left=null, right=null}} L:null R:null 每个节点的输出 TreeNode{val=3, left=TreeNode{val=6, left=TreeNode{val=12, left=null, right=null}, right=TreeNode{val=13, left=null, right=null}}, right=TreeNode{val=7, left=TreeNode{val=14, left=null, right=null}, right=TreeNode{val=15, left=null, right=null}}} L:null R:null 每个节点的输出 TreeNode{val=1, left=TreeNode{val=2, left=TreeNode{val=4, left=TreeNode{val=8, left=null, right=null}, right=TreeNode{val=9, left=null, right=null}}, right=TreeNode{val=5, left=TreeNode{val=10, left=null, right=null}, right=TreeNode{val=11, left=null, right=null}}}, right=TreeNode{val=3, left=TreeNode{val=6, left=TreeNode{val=12, left=null, right=null}, right=TreeNode{val=13, left=null, right=null}}, right=TreeNode{val=7, left=TreeNode{val=14, left=null, right=null}, right=TreeNode{val=15, left=null, right=null}}}} L:TreeNode{val=2, left=TreeNode{val=4, left=TreeNode{val=8, left=null, right=null}, right=TreeNode{val=9, left=null, right=null}}, right=TreeNode{val=5, left=TreeNode{val=10, left=null, right=null}, right=TreeNode{val=11, left=null, right=null}}} R:null
代码展示:
使用递归的方式:
//时间6 ms击败99.98% //内存43 MB击败27.84% //递归的优雅写法 class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { // 首先这里是如果找到一个节点符合就要进行返回 if (root == null || p == root || q == root) { return root; } //走到这一步说明 该节点不符合任意目标节点所以遍历他的子节点 TreeNode l = lowestCommonAncestor(root.left, p, q); TreeNode r = lowestCommonAncestor(root.right, p, q); // 那么返回情况分为三种: // 左边或者右边是null,这说明某一边是没有目标值的,说明该节点不是最近公共先祖 // 最近公共先祖是该节点的子节点,故要返回子节点 // 左边和右边都是不是null,则说明目标节点刚好在我的左右两边,则我是他们的最近公共先祖,理应返回自身 return l == null ? r : (r == null ? l : root); } }
暴力的全遍历的方式:
//时间10 ms击败14.27% //内存43.1 MB击败5.3% //时间复杂度:O(N),其中 N 是二叉树的节点数。 //二叉树的所有节点有且只会被访问一次,从 p 和 q 节点往上跳经过的祖先节点个数不会超过 N,因此总的时间复杂度为 O(N)。 //空间复杂度:O(N) ,其中 N 是二叉树的节点数。 //递归调用的栈深度取决于二叉树的高度,二叉树最坏情况下为一条链,此时高度为 N,因此空间复杂度为 O(N),哈希表存储每个节点的父节点也需要 O(N) 的空间复杂度,因此最后总的空间复杂度为 O(N)。 /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { Map<Integer, TreeNode> parent = new HashMap<Integer, TreeNode>(); Set<Integer> visited = new HashSet<Integer>(); public void dfs(TreeNode root) { if (root.left != null) { parent.put(root.left.val, root); dfs(root.left); } if (root.right != null) { parent.put(root.right.val, root); dfs(root.right); } } public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { dfs(root); while (p != null) { visited.add(p.val); p = parent.get(p.val); } while (q != null) { if (visited.contains(q.val)) { return q; } q = parent.get(q.val); } return null; } }

