剑指 Offer 27. 二叉树的镜像（226. 翻转二叉树）

题目：

 

 

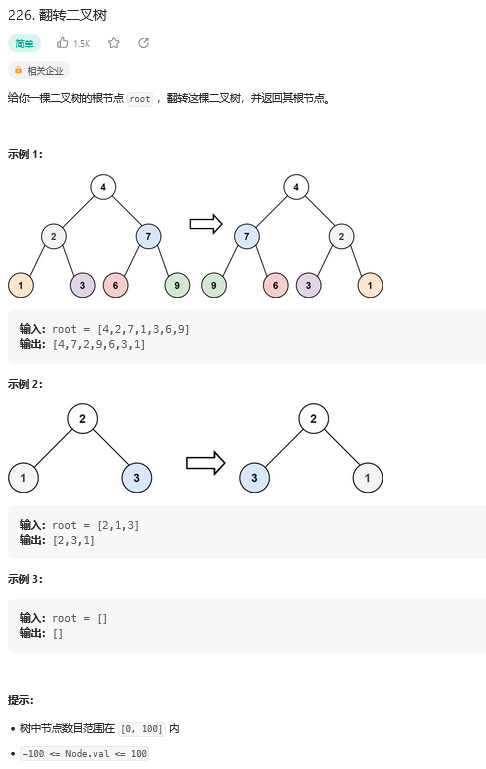
思路：

【1】这道题本身有点类似于判断是否为（101. 对称二叉树） ，不过本身的话其实也是考虑能不能在原本的节点上变化，还是必须要开一棵新树。而且基于递归的方式是最简单的，虽然容易造成递归层次很深，但是用循环遍历树有些情况确实不好搞。

代码展示：

//时间0 ms击败100%
//内存39.2 MB击败20.65%
//这种是拷贝出一颗新的树，不改动原有的树
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if (root == null) return null;
        TreeNode newTree = new TreeNode(root.val);
        copyTree(root,newTree);
        return newTree;
    }

    public void copyTree(TreeNode oldRoot,TreeNode newRoot) {
        if (oldRoot == null) return;
        if (oldRoot.left != null) {
            newRoot.right = new TreeNode(oldRoot.left.val);
            copyTree(oldRoot.left,newRoot.right);
        }
        if (oldRoot.right != null) {
            newRoot.left = new TreeNode(oldRoot.right.val);
            copyTree(oldRoot.right,newRoot.left);
        }
    }
}

//时间0 ms击败100%
//内存39.1 MB击败30.10%
//时间复杂度：O(N)，其中 N 为二叉树节点的数目。
//我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树。
//空间复杂度：O(N)O(N)O(N)。使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。
//在平均情况下，二叉树的高度与节点个数为对数关系，即 O(log⁡N)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

//这种是在原本的树上进行变换，然后返回还是那个头节点
class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if (root == null)  return null;
        if (root.left == null && root.right == null) return root;
        TreeNode left = mirrorTree(root.left);
        TreeNode right = mirrorTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}