剑指 Offer 55 - II. 平衡二叉树（110. 平衡二叉树）

题目：

 

 

 

 

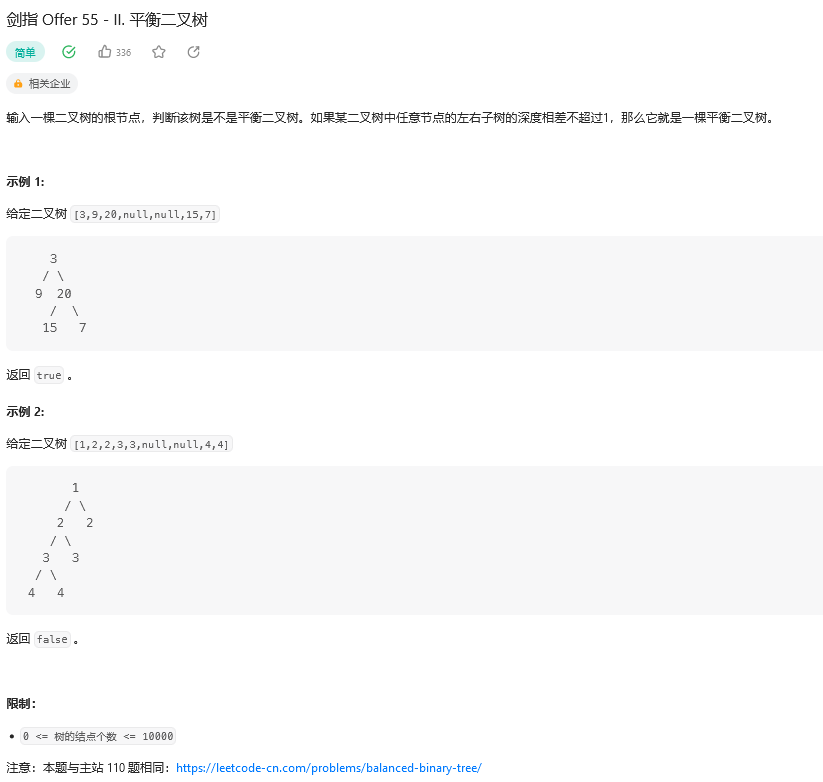
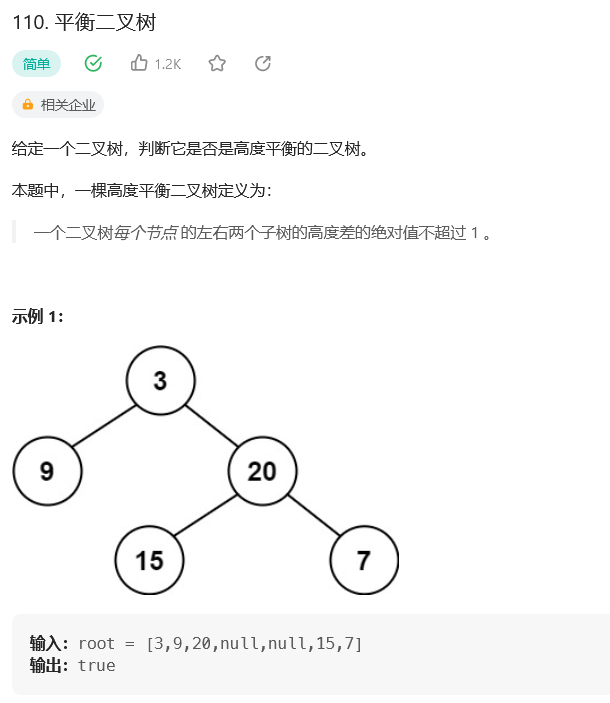
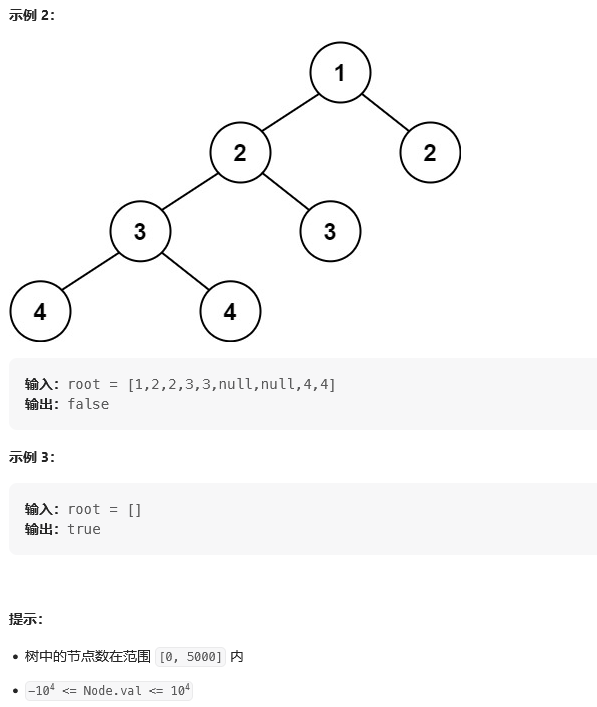
思路：

【1】自顶向下的递归

【2】自底向上的递归

代码展示：

自底向上的递归的方式：

//时间0 ms击败100%
//内存41.1 MB击败52.64%
class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) >= 0;
    }

    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = height(root.left);
        int rightHeight = height(root.right);
        if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}

优化一点的写法：
class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }
        if (isBalanced(root.left) && isBalanced(root.right)) {
            int left = root.left == null ? 1 : root.left.val;
            int right = root.right == null ? 1 : root.right.val;
            root.val = Math.max(left, right) + 1;
            return Math.abs(left - right) <= 1;
        }
        return false;
    }
}

 

自顶向下的递归的方式：

//时间1 ms击败45.78%
//内存41.2 MB击败43.78%
//时间复杂度：O(n^2)，其中 n 是二叉树中的节点个数。 
//最坏情况下，二叉树是满二叉树，需要遍历二叉树中的所有节点，时间复杂度是 O(n)。
//对于节点 p，如果它的高度是 d，则 height(p) 最多会被调用 d 次（即遍历到它的每一个祖先节点时）。
//对于平均的情况，一棵树的高度 h 满足 O(h)=O(log⁡n)，因为 d≤h ，所以总时间复杂度为 O(nlog⁡n)。
//对于最坏的情况，二叉树形成链式结构，高度为 O(n)，此时总时间复杂度为 O(n^2)。
//空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        } else {
            return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
        }
    }

    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            return Math.max(height(root.left), height(root.right)) + 1;
        }
    }
}