剑指 Offer 62. 圆圈中最后剩下的数字(约瑟夫环问题)
题目:
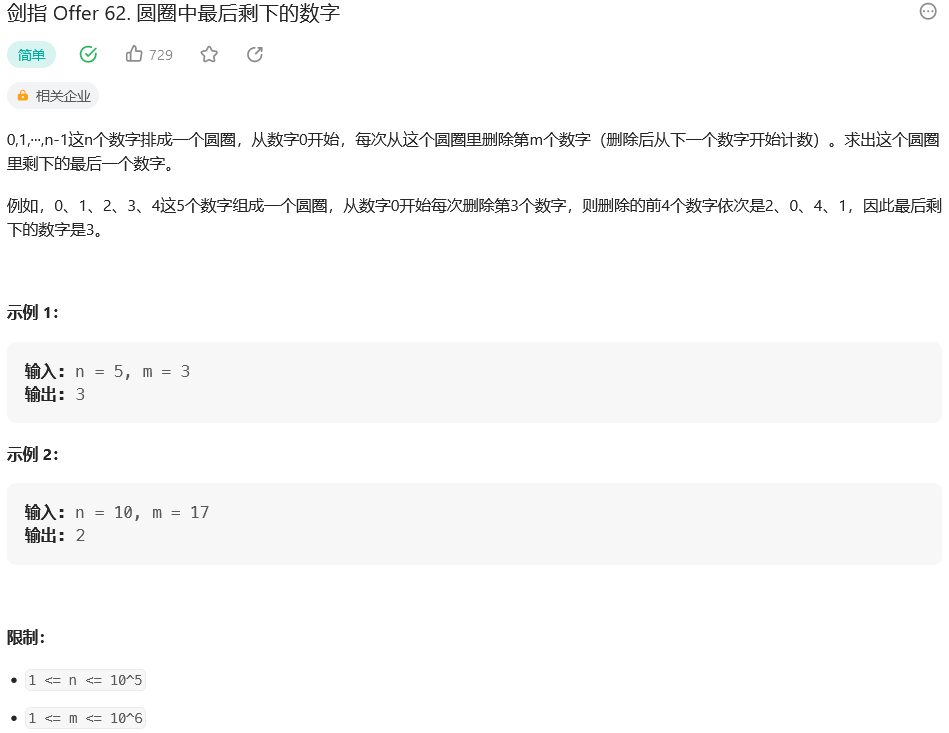
思路:
【1】纯粹的模拟法
【2】数学解法,O(n)
示例:[0, 1, 2, 3, 4]
从最后剩下的 3 倒着看,我们可以反向推出这个数字在之前每个轮次的位置。
最后剩下的 3 的下标是 0。
第四轮反推,补上 mmm 个位置,然后模上当时的数组大小 222,位置是(0 + 3) % 2 = 1。
第三轮反推,补上 mmm 个位置,然后模上当时的数组大小 333,位置是(1 + 3) % 3 = 1。
第二轮反推,补上 mmm 个位置,然后模上当时的数组大小 444,位置是(1 + 3) % 4 = 0。
第一轮反推,补上 mmm 个位置,然后模上当时的数组大小 555,位置是(0 + 3) % 5 = 3。
所以最终剩下的数字的下标就是3。因为数组是从0开始的,所以最终的答案就是3。
总结一下反推的过程,就是 (当前index + m) % 上一轮剩余数字的个数。
代码展示:
//时间1056 ms击败9.82% //内存44 MB击败5.13% class Solution { public int lastRemaining(int n, int m) { ArrayList<Integer> list = new ArrayList<>(n); for (int i = 0; i < n; i++) { list.add(i); } int idx = 0; while (n > 1) { idx = (idx + m - 1) % n; list.remove(idx); n--; } return list.get(0); } } //时间4 ms击败98.93% //内存38.3 MB击败76.26% class Solution { public int lastRemaining(int n, int m) { int ans = 0; // 最后一轮剩下2个人,所以从2开始反推 for (int i = 2; i <= n; i++) { ans = (ans + m) % i; } return ans; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号