31. 下一个排列

题目：

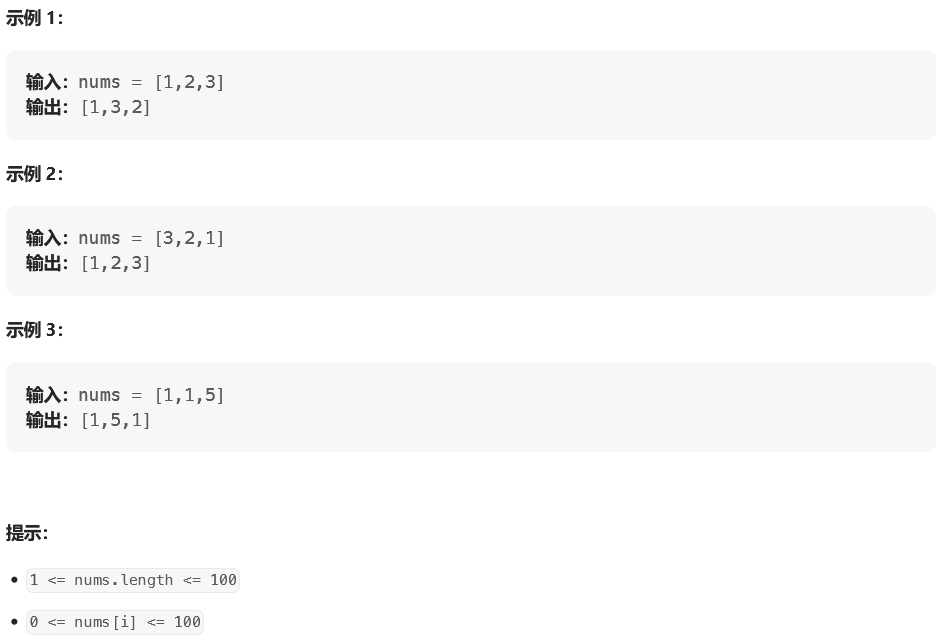
思路：

【1】“下一个排列” 的定义是：给定数字序列的字典序中下一个更大的排列。如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）

【2】如何得到这样的排列顺序

1)希望下一个数 比当前数大，这样才满足 “下一个排列” 的定义。
因此只需要 将后面的「大数」与前面的「小数」交换，就能得到一个更大的数。
如 123456，将 5 和 6 交换就能得到一个更大的数 123465。

2)我们还希望下一个数 增加的幅度尽可能的小，这样才满足“下一个排列与当前排列紧邻“的要求。
为了满足这个要求，我们需要：
    (1)在 尽可能靠右的低位 进行交换，需要 从后向前 查找
    (2)将一个 尽可能小的「大数」 与前面的「小数」交换。比如 123465，下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换
    (3)将「大数」换到前面后，需要将「大数」后面的所有数 重置为升序，升序排列就是最小的排列。
    以 123465 为例：
        首先按照上一步，交换 5 和 4，得到 123564；
        然后需要将 5 之后的数重置为升序，得到 123546。
        显然 123546 比 123564 更小，123546 就是 123465 的下一个排列

 

【3】标准的 “下一个排列” 算法可以描述为：

1）从后向前 查找第一个 相邻升序 的元素对 (i,j)，满足 A[i] < A[j]。此时 [j,end) 必然是降序
2）在 [j,end) 从后向前 查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
3）将 A[i] 与 A[k] 交换
4）可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序
5）如果在步骤 1 找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到步骤 4

 

 

代码展示：

//时间0 ms击败100%
//内存41.9 MB击败41.18%
//时间复杂度：O(N)，其中 N 为给定序列的长度。我们至多只需要扫描两次序列，以及进行一次反转操作。
//空间复杂度：O(1)，只需要常数的空间存放若干变量。
class Solution {
    public void nextPermutation(int[] nums) {
        int i = nums.length - 2;
        //判断是不是已经是降序排序了，是的话，就已经是最大排列，需要进行反转
        //
        while (i >= 0 && nums[i] >= nums[i + 1]) {
            i--;
        }
        if (i >= 0) {
            int j = nums.length - 1;
            while (j >= 0 && nums[i] >= nums[j]) {
                j--;
            }
            swap(nums, i, j);
        }
        reverse(nums, i + 1);
    }

    public void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    public void reverse(int[] nums, int start) {
        int left = start, right = nums.length - 1;
        while (left < right) {
            swap(nums, left, right);
            left++;
            right--;
        }
    }
}