剑指 Offer 33. 二叉搜索树的后序遍历序列

题目：

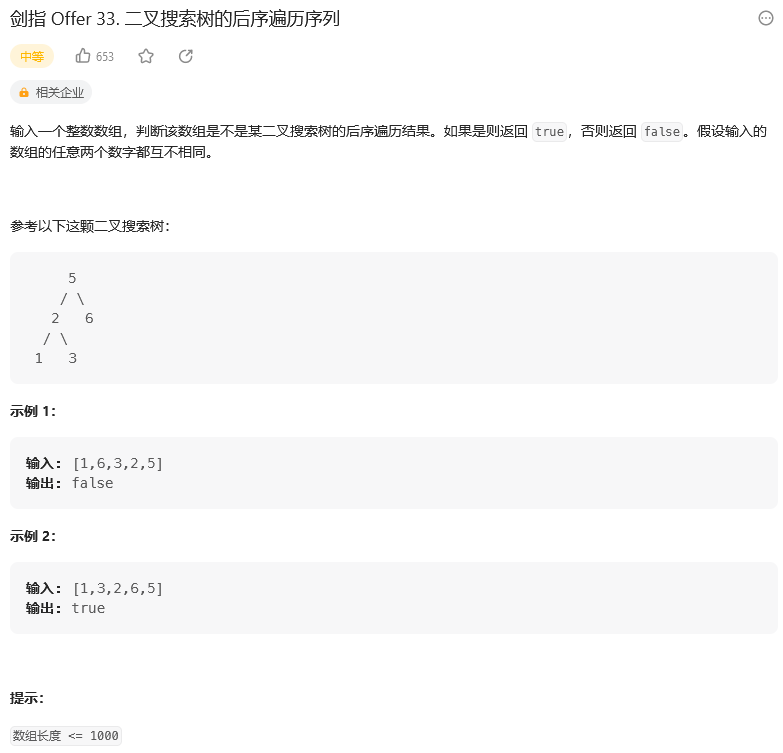
思路：

【1】后序遍历定义： [ 左子树 | 右子树 | 根节点 ] ，即遍历顺序为 “左、右、根” 。

【2】二叉搜索树定义： 左子树中所有节点的值 < 根节点的值；右子树中所有节点的值 > 根节点的值；其左、右子树也分别为二叉搜索树。

【3】故可以采用递归的方式来进行处理：

采用递归的话，划分就很重要了
如：树结构为
     5
    / \
   2   6
  / \
 1   3
在数组中为 arr = [1,3,2,6,5]
那要怎么划分呢，首先根节点必然在最后，故直接root = arr[arr.length - 1]就可以取出来
那么剩下的[1,3,2,6]如何划分左右子树呢，
其实从左和从右都可以，假设从左，i=0
当arr[i] < root ,则arr[i]是属于左子树的，i++，判断下一个，直到不满足条件时，就是已经遍历到右子树的节点了
那么剩下的就要判断arr[i] > root .
当然我们要知道，如果是满足后序遍历的话，必然可以遍历完，除根节点以外的其他节点，否则这就不满足后序遍历了。

 

【4】使用辅助空间栈来替换递归：

翻转先序遍历又是root->right->left的，基于这样的性质和遍历方式，我们知道越往右越大，这样，就可以构造一个单调递增的栈，来记录遍历的元素。

为什么要用单调栈呢，因为往右子树遍历的过程，value是越来越大的，一旦出现了value小于栈顶元素value的时候，就表示要开始进入左子树了
（如果不是，就应该继续进入右子树，否则不满足二叉搜索树的定义，不理解的请看下二叉搜索树的定义），但是这个左子树是从哪个节点开始的呢？

单调栈帮我们记录了这些节点，只要栈顶元素还比当前节点大，就表示还是右子树，要移除，因为我们要找到这个左孩子节点直接连接的父节点，也就是找到这个子树的根，
只要栈顶元素还大于当前节点，就要一直弹出，直到栈顶元素小于节点，或者栈为空。栈顶的上一个元素就是子树节点的根。

接下来，数组继续往前遍历，之后的左子树的每个节点，都要比子树的根要小，才能满足二叉搜索树，否则就不是二叉搜索树

 

代码展示：

使用栈的辅助空间：

//时间1 ms击败22.71%
//内存38.7 MB击败92.61%
//时间复杂度 O(N) ： 遍历 postorder 所有节点，各节点均入栈 / 出栈一次，使用 O(N) 时间。
//空间复杂度 O(N) ： 最差情况下，单调栈 stack 存储所有节点，使用 O(N) 额外空间。
class Solution {
    public boolean verifyPostorder(int[] postorder) {
        // 单调栈使用，单调递增的单调栈
        Deque<Integer> stack = new LinkedList<>();
        int pervElem = Integer.MAX_VALUE;
        // 逆向遍历，就是翻转的先序遍历
        for (int i = postorder.length - 1;i>=0;i--){
            // 左子树元素必须要小于递增栈被peek访问的元素，否则就不是二叉搜索树
            if (postorder[i] > pervElem){
                return false;
            }
            while (!stack.isEmpty() && postorder[i] < stack.peek()){
                // 数组元素小于单调栈的元素了，表示往左子树走了，记录下上个根节点
                // 找到这个左子树对应的根节点，之前右子树全部弹出，不再记录，因为不可能在往根节点的右子树走了
                pervElem = stack.pop();
            }
            // 这个新元素入栈
            stack.push(postorder[i]);
        }
        return true;
    }
}

 

 

基于递归的方式：

//时间0 ms击败100%
//内存39.4 MB击败7.30%
//时间复杂度 O(N^2) ： 每次调用 recur(i,j) 减去一个根节点，因此递归占用 O(N) ；最差情况下（即当树退化为链表），每轮递归都需遍历树所有节点，占用 O(N) 。
//空间复杂度 O(N) ： 最差情况下（即当树退化为链表），递归深度将达到 N 。
class Solution {
    public boolean verifyPostorder(int[] postorder) {
        return recur(postorder, 0, postorder.length - 1);
    }

    public boolean recur(int[] postorder, int i, int j) {
        //这是递归的终止条件，
        if(i >= j) return true;

        //基于左子树都比根节点小的理论找出所有归属左子树的节点
        int p = i;
        while(postorder[p] < postorder[j]) p++;

        //基于右子树都比根节点大的理论找出所有归属右子树的节点
        int m = p;
        while(postorder[p] > postorder[j]) p++;

        //这里的p == j，是为了判断如果存在节点不满足规律导致其他节点不能进行左右划分那么这个必然不能算是二叉树的后序遍历
        //如果满足的话就继续划分
        return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
    }
}