剑指 Offer 66. 构建乘积数组（238. 除自身以外数组的乘积）

题目：

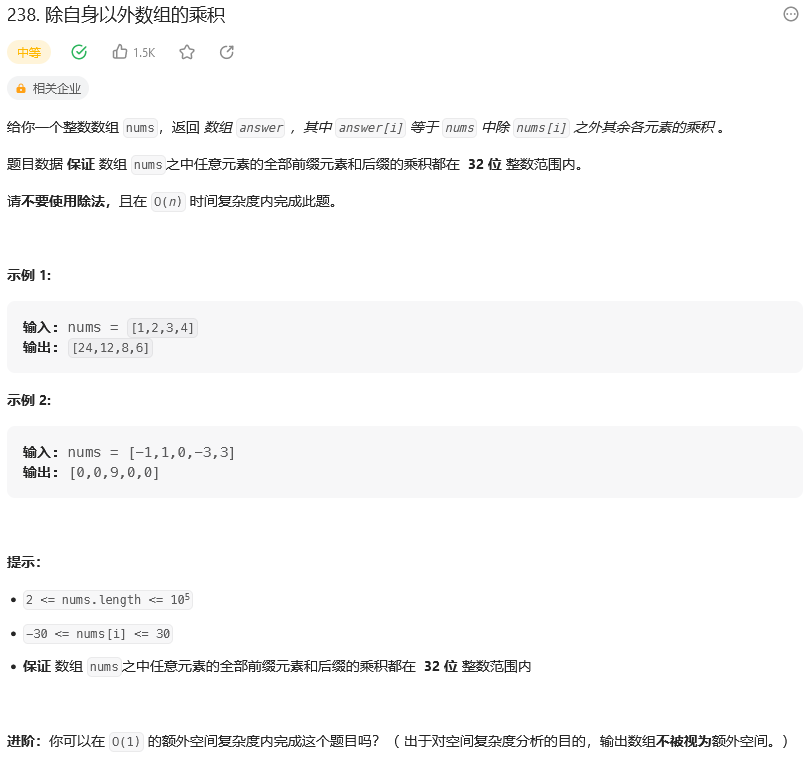
思路：

【1】构建乘积列表的方式，这种本身就是基于除法的思想，相比于暴力破解要进行多次计算，倒不如，遍历一次，然后进行除法，得到结果。可惜由于输入会存在0，所以除法是禁止的，但是问题不大，构建两个乘积表呗，一个记录左边乘积，一个记录右边乘积，然后结果便是将左乘积表的值和右乘积表的值拿出来相乘便是答案了，最多是由原本的两次循环变成了三次，一个N的辅助空间变量变为2N的空间辅助变量。本质上和用除法的空间复杂度和时间复杂度都是一样的，甚至计算过程远比暴力破解的方式更加节省。毕竟采用了空间换时间。毕竟N^2在当数据大到万级的时候光是计算就要花费很多时间。

【2】在构建乘积表的思路上再进行优化。在写构建乘积表的过程我们很容易发现并不一定要把表构建出来，因为本身就可以使用单个辅助变量记录当前下标的左边或者右边的乘积，那么我们是不是直接相乘存入结果数组中就可以了，这样一想貌似又是可以的，那么对于遍历次数也可以减少了，空间变量也减少了。

代码展示：

在构建乘积表的思路上再进行优化：

//时间1 ms击败100%
//内存52.3 MB击败45.58%
//时间复杂度：O(N)，其中 N 指的是数组 a 的大小。
//空间复杂度：O(1)。输出数组不算进空间复杂度中，因此我们只需要常数的空间存放变量。
class Solution {
    public int[] constructArr(int[] a) {
        //防止输入 a = {}的时候下面指定下标的地方会出现溢出
        if (a == null || a.length == 0){
            return a;
        }
        
        int length = a.length;
        int[] answer = new int[length];

        // answer[i] 表示索引 i 左侧所有元素的乘积
        // 因为索引为 '0' 的元素左侧没有元素， 所以 answer[0] = 1
        answer[0] = 1;
        for (int i = 1; i < length; i++) {
            answer[i] = a[i - 1] * answer[i - 1];
        }

        // R 为右侧所有元素的乘积
        // 刚开始右边没有元素，所以 R = 1
        int R = 1;
        for (int i = length - 1; i >= 0; i--) {
            // 对于索引 i，左边的乘积为 answer[i]，右边的乘积为 R
            answer[i] = answer[i] * R;
            // R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
            R *= a[i];
        }
        return answer;
    }
}

 

构建左右乘积列表：

//时间1 ms击败100%
//内存51.8 MB击败73.2%
//时间复杂度：O(N)，其中 N 指的是数组 a 的大小。预处理 L 和 R 数组以及最后的遍历计算都是 O(N) 的时间复杂度。
//空间复杂度：O(N)，其中 N 指的是数组 a 的大小。使用了 L 和 R 数组去构造答案，L 和 R 数组的长度为数组 a 的大小。
class Solution {
    public int[] constructArr(int[] a) {
        //防止输入 a = {}的时候下面指定下标的地方会出现溢出
        if (a == null || a.length == 0){
            return a;
        }
        int length = a.length;

        // L 和 R 分别表示左右两侧的乘积列表
        int[] L = new int[length];
        int[] R = new int[length];

        int[] res = new int[length];
        // L[i] 为索引 i 左侧所有元素的乘积
        // 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
        L[0] = 1;
        for (int i = 1; i < length; i++) {
            L[i] = a[i - 1] * L[i - 1];
        }

        // R[i] 为索引 i 右侧所有元素的乘积
        // 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
        R[length - 1] = 1;
        for (int i = length - 2; i >= 0; i--) {
            R[i] = a[i + 1] * R[i + 1];
        }

        // 对于索引 i，除 a[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
        for (int i = 0; i < length; i++) {
            res[i] = L[i] * R[i];
        }

        return res;
    }
}

//时间2 ms击败26.94%
//内存51.5 MB击败86.96%
//当然这种是相对于上面的另一种处理，就是在循环中增加判断，虽然也可以但是性能的话相对于上面这种肯定是有对应损耗的。但是胜在写的时候行数会少一点，代码简短。
class Solution {
    public int[] constructArr(int[] a) {
        int length = a.length;

        // L 和 R 分别表示左右两侧的乘积列表
        int[] L = new int[length];
        int[] R = new int[length];
        int[] res = new int[length];
        // L[i] 为索引 i 左侧所有元素的乘积
        // 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
        for (int i = 0; i < length; i++) {
            L[i] = i == 0 ? 1 : a[i - 1] * L[i - 1];
        }

        // R[i] 为索引 i 右侧所有元素的乘积
        // 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
        for (int i = length - 1; i >= 0; i--) {
            R[i] = i == length - 1 ? 1 : a[i + 1] * R[i + 1];
        }

        // 对于索引 i，除 a[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
        for (int i = 0; i < length; i++) {
            res[i] = L[i] * R[i];
        }

        return res;
    }
}

 

会出现问题的情况：

双循环暴力破解的方式：
//会出现超出时间限制的问题
class Solution {
    public int[] constructArr(int[] a) {
        int[] res = new int[a.length];
        int count;
        for (int i = 0; i < a.length; i++){
            count = 1;
            for (int j = 0; j < a.length; j++){
                if (i!=j){
                    count *= a[j];
                }
            }
            res[i] = count;
        }
        return res;
    }
}

当然是用除法的话：
//当输入存在0的情况，如[1, 2, 0, 4, 5]，出现异常java.lang.ArithmeticException: / by zero
class Solution {
    public int[] constructArr(int[] a) {
        int[] res = new int[a.length];
        int count = 1;
        for (int i = 0; i < a.length; i++){
            count *= a[i];
        }
        for (int i = 0; i < a.length; i++){
            res[i] = count/a[i];
        }
        return res;
    }
}