剑指 Offer 36. 二叉搜索树与双向链表（426. 将二叉搜索树转化为排序的双向链表）

题目：

思路：

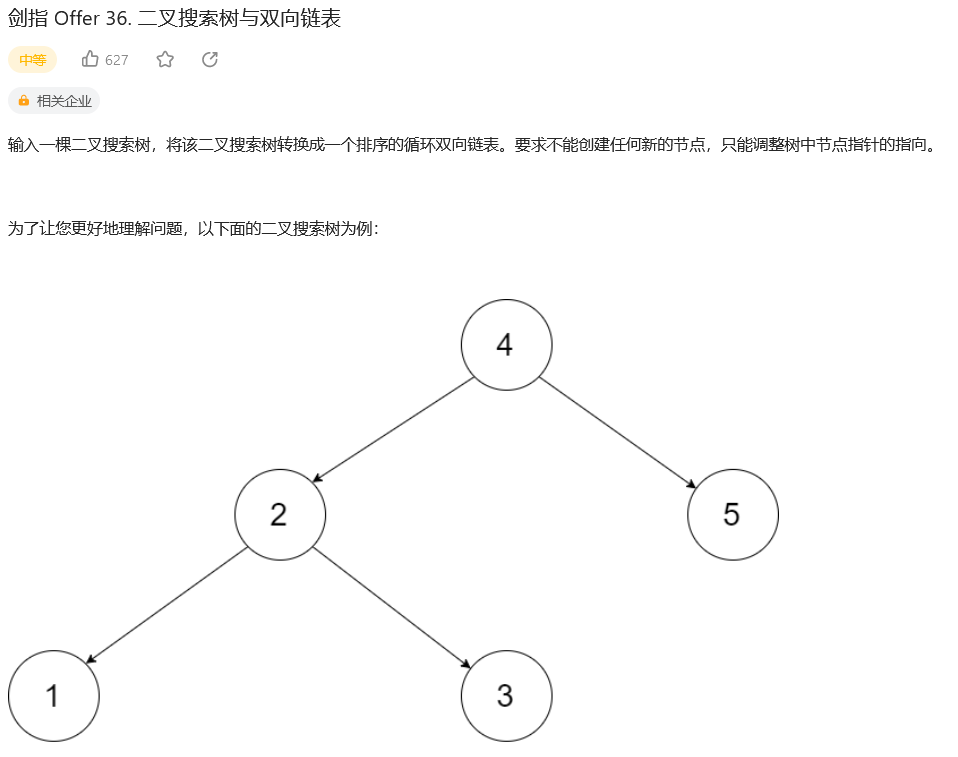
【1】这道题本身的思路就是对树进行中序遍历，然后将其按中序遍历的顺序变成链表，而且在于不能创建新的节点：

【2】递归是最为简单的中序遍历：

// 打印中序遍历
void dfs(Node root) {

    if(root == null) return;

    dfs(root.left); // 左

    System.out.println(root.val); // 根

    dfs(root.right); // 右

}

 

【3】最简单的方法就是利用辅助空间进行记录中序遍历的节点指向，全部记录下来后再进行变更左右节点的指引。但这种消耗的空间有点大，不是最优的。

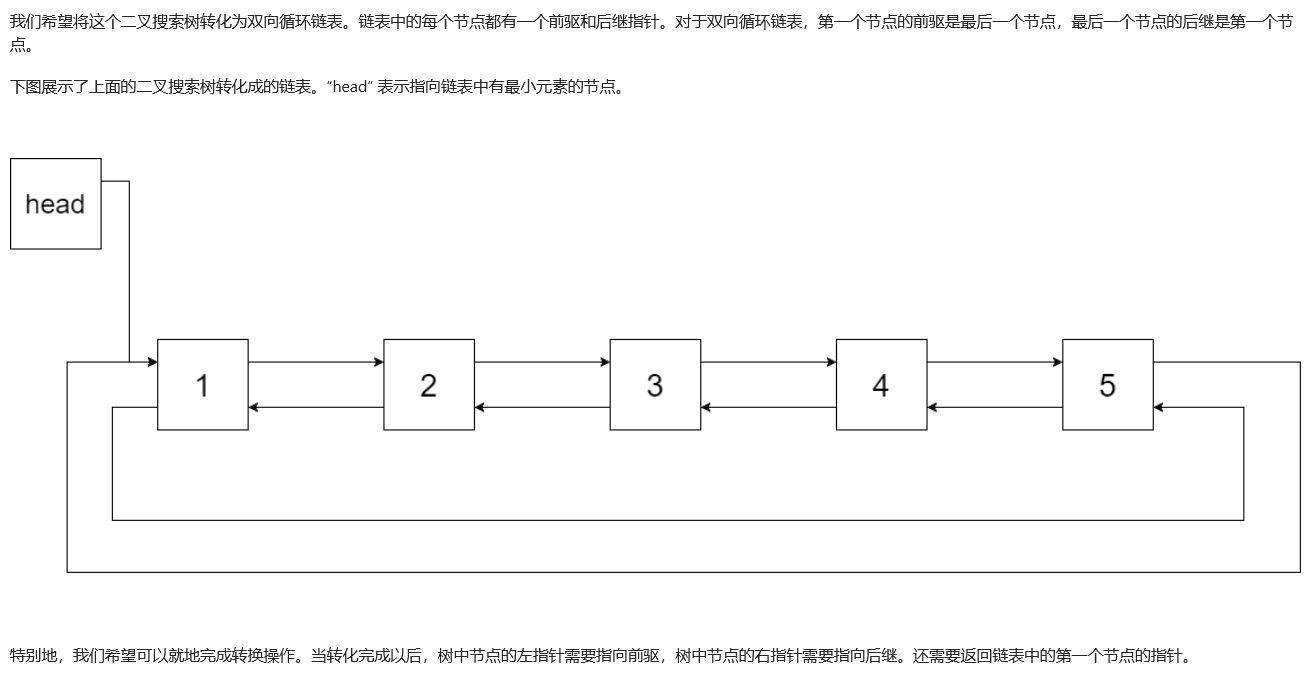
【4】优化一点的就可以采用两个节点变量，head和pre，pre是表示当前节点的上一个节点，head表示头结点，cur表示当前节点。如果pre=null，就代表还没设置头结点。所以此时要设置head节点，其次，操作完后要设置pre=cur，因为cur会是下一个节点的pre，所以除了一开始pre会是null，后面都不会为null。而且在最后的时候因为最后一个右结点的指向是null，所以pre就会指向最后的右结点。故一切就会变得简单了起来。

 

代码展示：

借助两个变量进行对树转成双向链表：

//时间0 ms击败100%
//内存41 MB击败42.56%
//时间复杂度 O(N) ： N 为二叉树的节点数，中序遍历需要访问所有节点。
//空间复杂度 O(N) ： 最差情况下，即树退化为链表时，递归深度达到 N，系统使用 O(N) 栈空间。
/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
    Node pre, head;

    public Node treeToDoublyList(Node root) {

        if(root == null) return null;

        dfs(root);

        head.left = pre;

        pre.right = head;

        return head;

    }

    void dfs(Node cur) {

        if(cur == null) return;

        dfs(cur.left);
        
        //pre用于记录双向链表中位于cur左侧的节点，即上一次迭代中的cur,当pre==null时，cur左侧没有节点,即此时cur为双向链表中的头节点
        if(pre==null) head = cur;
        //反之，pre!=null时，cur左侧存在节点pre，需要进行pre.right=cur的操作。
        else pre.right = cur;
        cur.left = pre;//pre是否为null对这句没有影响,且这句放在上面两句if else之前也是可以的。
        pre = cur;//pre指向当前的cur

        dfs(cur.right);//全部迭代完成后，pre指向双向链表中的尾节点

    }
}

当然如果看起来比较模糊的话，换另一中写法可能更清晰：

public void dfs(Node root){
    if(root==null) return;
    dfs(root.left);
    if(pre==null){
        head = root;
        pre = head;
    }else{
        pre.right = root;
        root.left = pre;
        pre = root;
    } 
    dfs(root.right);
}