剑指 Offer 38. 字符串的排列（比较难懂）

题目：

思路：

【1】利用递归回溯的方式：

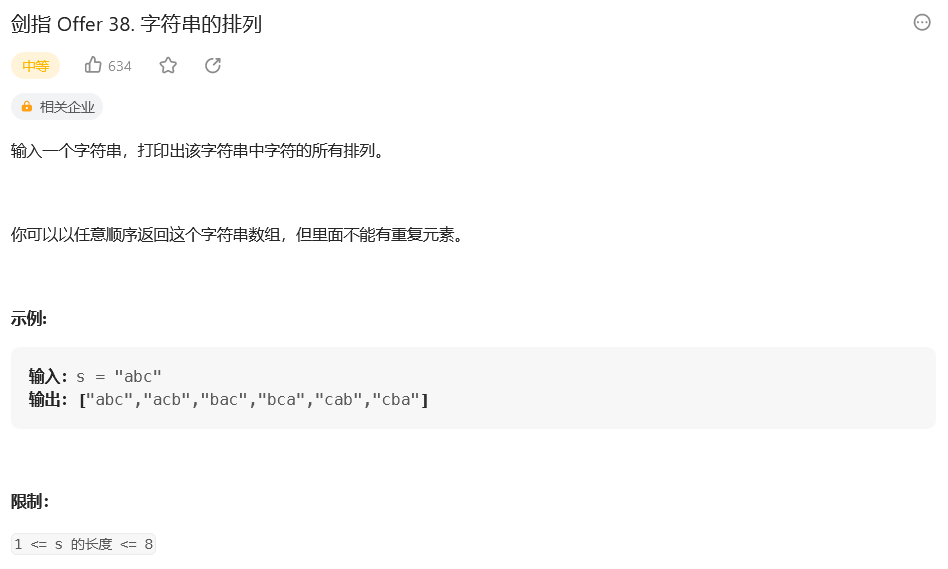
排列方案的生成【基本上是基于确定第一个，然后到确定第二个，...，再到确认最后一个（这里面涉及到了递归和循环，因为递归是一层层，而循环代表着这一层的可能性）】：

 

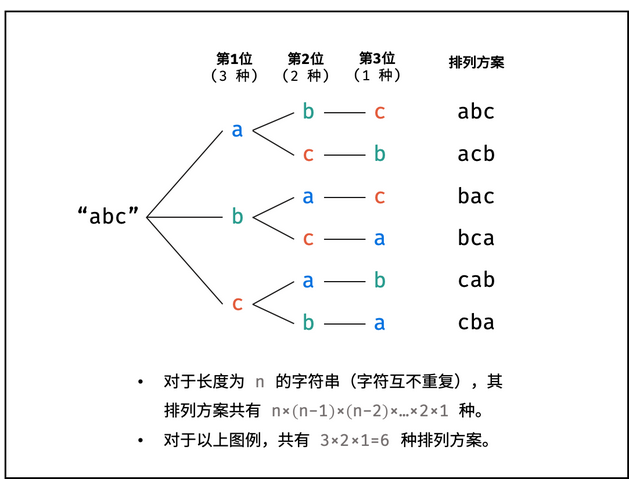
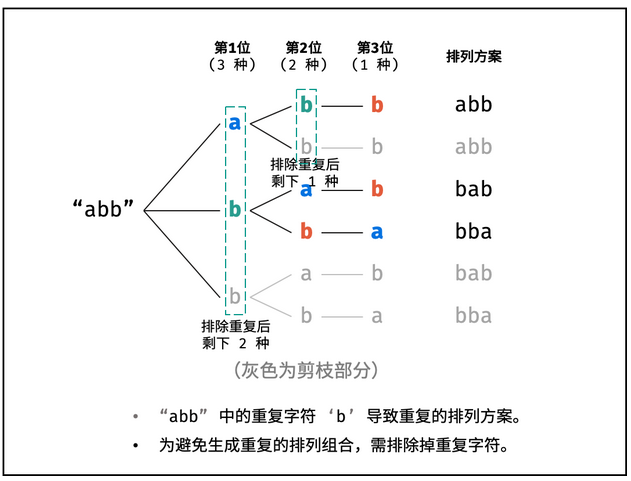
重复排列方案与剪枝【剪枝表示同一层遇到了放在同一位置的相同字符，这种应该跳过，从二叉树的角度的话是去除掉这一分支，类似于减去树枝的一部分】：

 

 

【2】利用之前遇到的获取下一个排序的方法，将全部排序获取出来，参考  31. 下一个排列 ：

代码展示：

利用获取下一个排序的方式：

//时间8 ms击败75.35%
//内存45.9 MB击败85.72%
//时间复杂度：O(n×n!)，其中 n 为给定字符串的长度。我们需要 O(nlog⁡n) 的时间得到第一个排列，nextPermutation 函数的时间复杂度为 O(n)，我们至多执行该函数 O(n!) 次，因此总时间复杂度为 O(n×n!+nlog⁡n)=O(n×n!)。
//空间复杂度：O(1)。注意返回值不计入空间复杂度。
class Solution {
    public String[] permutation(String s) {
        List<String> ret = new ArrayList<String>();
        char[] arr = s.toCharArray();
        //将字符串升序排列，这样就是最小的时候
        Arrays.sort(arr);
        //先添加入数组，再判断是否还存在下一个更大一点的，有就塞入数组
        do {
            ret.add(new String(arr));
        } while (nextPermutation(arr));
        int size = ret.size();
        String[] retArr = new String[size];
        for (int i = 0; i < size; i++) {
            retArr[i] = ret.get(i);
        }
        return retArr;
    }

    public boolean nextPermutation(char[] arr) {
        int i = arr.length - 2;
        while (i >= 0 && arr[i] >= arr[i + 1]) {
            i--;
        }
        if (i < 0) {
            return false;
        }
        int j = arr.length - 1;
        while (j >= 0 && arr[i] >= arr[j]) {
            j--;
        }
        swap(arr, i, j);
        reverse(arr, i + 1);
        return true;
    }
    //交换位置函数
    public void swap(char[] arr, int i, int j) {
        char temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    //进行字符串反转
    public void reverse(char[] arr, int start) {
        int left = start, right = arr.length - 1;
        while (left < right) {
            swap(arr, left, right);
            left++;
            right--;
        }
    }
}

 

 

利用递归回溯的方式处理：

//时间7 ms击败88.54%
//内存47 MB击败21.45%
//时间复杂度 O(N!N) ： N 为字符串 s 的长度；时间复杂度和字符串排列的方案数成线性关系，方案数为 N×(N−1)×(N−2)…×2×1 ，即复杂度为 O(N!) ；字符串拼接操作 join() 使用 O(N) ；因此总体时间复杂度为 O(N!N) 。
//空间复杂度 O(N^2) ： 全排列的递归深度为 N ，系统累计使用栈空间大小为 O(N) ；递归中辅助 Set 累计存储的字符数量最多为 N+(N−1)+...+2+1=(N+1)N/2 ，即占用 O(N^2) 的额外空间。
class Solution {
    List<String> res = new LinkedList<>();
    char[] c;

    public String[] permutation(String s) {
        c = s.toCharArray();
        dfs(0);
        return res.toArray(new String[res.size()]);
    }

    public void dfs(int x) {
        if(x == c.length - 1) {
            res.add(String.valueOf(c));      // 添加排列方案
            return;
        }

        HashSet<Character> set = new HashSet<>();

        for(int i = x; i < c.length; i++) {
            if(set.contains(c[i])) continue; // 重复，因此剪枝
            set.add(c[i]);
            swap(i, x);                      // 交换，将 c[i] 固定在第 x 位
            dfs(x + 1);                      // 开启固定第 x + 1 位字符
            swap(i, x);                      // 恢复交换
        }

    }
    
    //位置交换函数
    public void swap(int a, int b) {
        char tmp = c[a];
        c[a] = c[b];
        c[b] = tmp;
    }
}

 

31. 下一个排列