剑指 Offer 49. 丑数（264. 丑数 II）

题目：

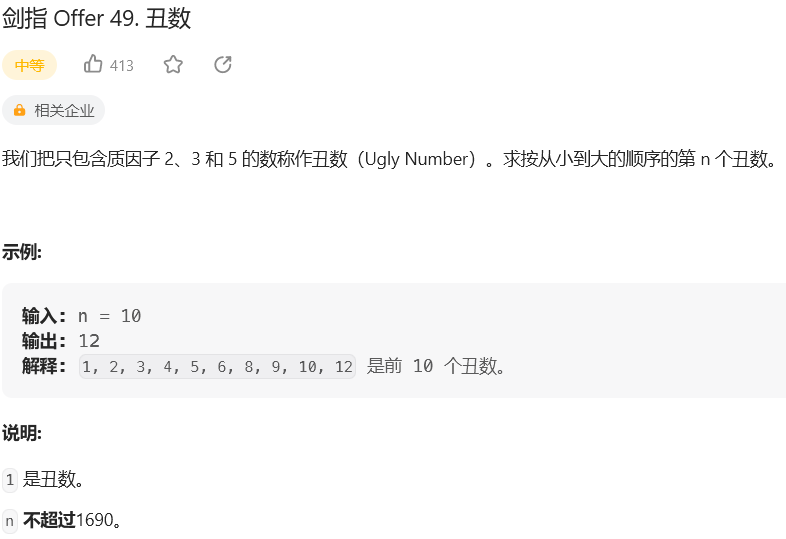
思路：

【1】理解丑数的形成，基础的有1,2,3,5。但后面的基本在于与前面的相乘如下一批为4,6,10和6,9,15。所以丑数基本是以基础数*2或者*3或者*5来找出来的。基于这个，大概可以考虑最小堆的方式，或者考虑辅助空间记录的方式。

【2】最小堆的思路，这个思路本质上不一定要刚好填到N个，而是可以填入3N，然后取出最小的N个即可，同理由于还会有重复的，所以还要去重。

【3】动态规划，其实就是很真实的给每个参数都记录下标。然后先取出最小的放入数组中，如果碰到重复的则要两者都移动一位。

代码展示：

动态规划的方式：

//时间2 ms击败98.37%
//内存39.9 MB击败31.72%
//时间复杂度：O(n)。需要计算数组 dp 中的 n 个元素，每个元素的计算都可以在 O(1) 的时间内完成。
//空间复杂度：O(n)。空间复杂度主要取决于数组 dp 的大小。
class Solution {
    public int nthUglyNumber(int n) {
        int[] dp = new int[n + 1];
        dp[1] = 1;
        int p2 = 1, p3 = 1, p5 = 1;
        for (int i = 2; i <= n; i++) {
            int num2 = dp[p2] * 2, num3 = dp[p3] * 3, num5 = dp[p5] * 5;
            dp[i] = Math.min(Math.min(num2, num3), num5);
            if (dp[i] == num2) {
                p2++;
            }
            if (dp[i] == num3) {
                p3++;
            }
            if (dp[i] == num5) {
                p5++;
            }
        }
        return dp[n];
    }
}

 

利用优先队列达到最小的堆的方式：

//时间51 ms击败9.45%
//内存41.3 MB击败12.52%
//时间复杂度：O(nlog⁡n)。
//得到第 n 个丑数需要进行 n 次循环，每次循环都要从最小堆中取出 1 个元素以及向最小堆中加入最多 3 个元素，因此每次循环的时间复杂度是 O(log⁡(3n)+3log⁡(3n))，总时间复杂度是O(n \log n)$。
//空间复杂度：O(n)。空间复杂度主要取决于最小堆和哈希集合的大小，最小堆和哈希集合的大小都不会超过 3n。
class Solution {
    public int nthUglyNumber(int n) {
        int[] factors = {2, 3, 5};
        Set<Long> seen = new HashSet<Long>();
        PriorityQueue<Long> heap = new PriorityQueue<Long>();
        seen.add(1L);
        heap.offer(1L);
        int ugly = 0;
        for (int i = 0; i < n; i++) {
            long curr = heap.poll();
            ugly = (int) curr;
            for (int factor : factors) {
                long next = curr * factor;
                if (seen.add(next)) {
                    heap.offer(next);
                }
            }
        }
        return ugly;
    }
}