剑指 Offer 44. 数字序列中某一位的数字（400. 第 N 位数字）

题目：

 

另一种说法：

 

思路：

【1】这道题如果没有了解到公式的话基本摸瞎，暴力破解超时不可用

【2】确定所求数位的所在数字的位数

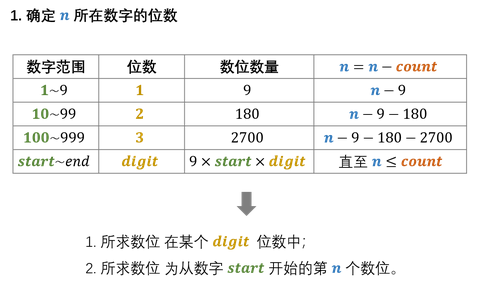
【3】确定所求数位所在的数字

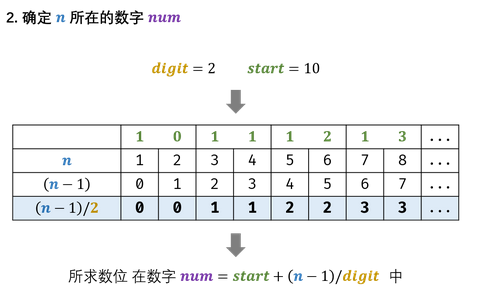
【4】确定所求数位在 numnumnum 的哪一数位

 

 

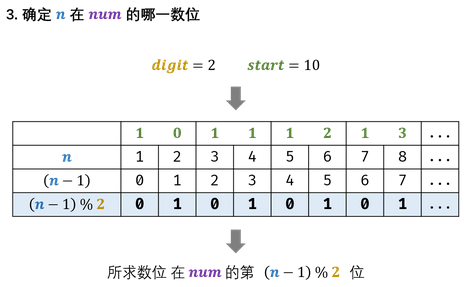
代码展示：

//时间0 ms击败100%
//内存38.2 MB击败79.88%
class Solution {
    public int findNthDigit(int n) {
        //先找出是几位数
        int digit = 1;
        long start = 1;
        long count = 9;
        while (n > count) {
            n -= count;
            digit += 1;
            start *= 10;
            count = digit * start * 9;
        }
        //确定所求数位所在的数字,start 为第 0 个数字
        long num = start + (n - 1) / digit;

        //确定所求数位在 numnumnum 的哪一数位
        return Long.toString(num).charAt((n - 1) % digit) - '0';
    }
}

//暴力的方式但是会超时
class Solution {
    public int findNthDigit(int n) {
        if (n == 0){
            return 0;
        }
        String temp;
        int res = -1;
        for (int i = 1; i < Integer.MAX_VALUE ; i++){
            temp = String.valueOf(i);
            if (n-temp.length() <= 0){
                System.out.println(temp);
                res = temp.charAt(n-1) - '0';
                break;
            }
            n = n-temp.length();
        }
        return res;
    }
}

//还有一种二分查找的方式，但是本质上还是根据数学公式推导出来
//说是二分，但其实也是先找出位置，更用公式推出来差不多，但是更加繁琐
class Solution {
    public int findNthDigit(int n) {
        int low = 1, high = 9;
        while (low < high) {
            int mid = (high - low) / 2 + low;
            if (totalDigits(mid) < n) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }
        int d = low;
        int prevDigits = totalDigits(d - 1);
        int index = n - prevDigits - 1;
        int start = (int) Math.pow(10, d - 1);
        int num = start + index / d;
        int digitIndex = index % d;
        return (num / (int) Math.pow(10, d - digitIndex - 1)) % 10;
    }
    public int totalDigits(int length) {
        int digits = 0;
        int curLength = 1, curCount = 9;
        while (curLength <= length) {
            digits += curLength * curCount;
            curLength++;
            curCount *= 10;
        }
        return digits;
    }
}