剑指 Offer II 004. 只出现一次的数字 （137. 只出现一次的数字 II）

题目：

思路：

【1】使用哈希辅助空间的简单处理，记录出现的次数，然后把次数为1的提取出来。

【2】转化为位数统计，因为转化成位数只有只有1和0，如果有1即代表出现一次，所以除以对应的次数得到的余数便是剩下的那个数字留下的。【这种和哈希辅助空间都是算是可以通用的，即使条件变化了，对应修改的依旧是次数，而次数其实可以提取出来作为通用变量】

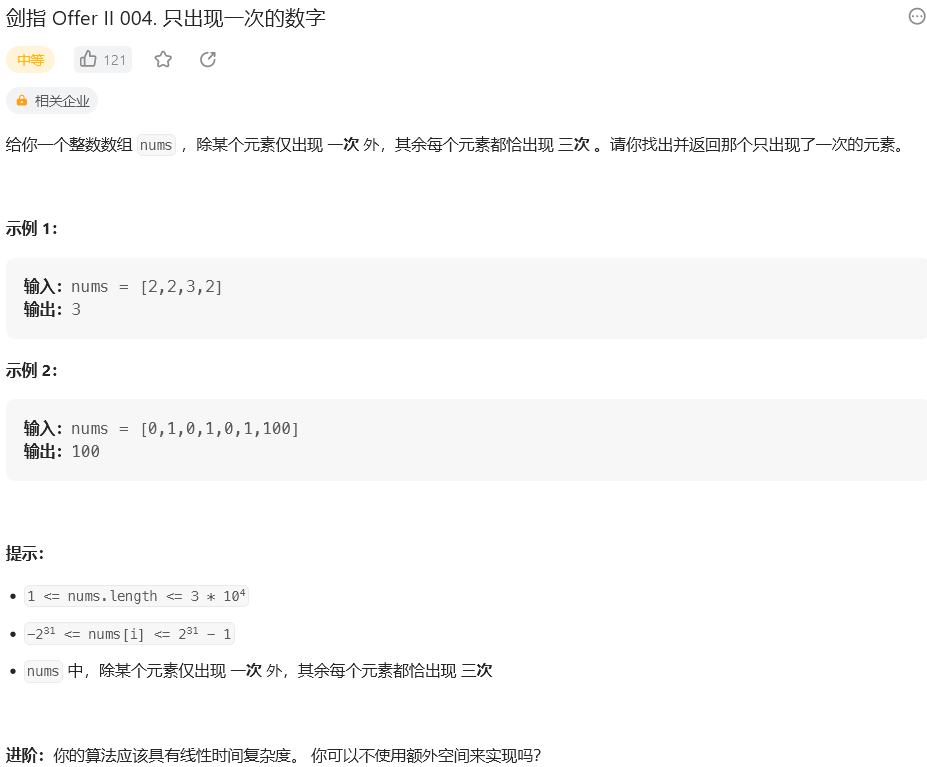
【3】最优的DFA（ Deterministic Finite Automaton 即确定有穷自动机），从一个状态通过一系列的事件转换到另一个状态。如当时出现两个的时候，利用相同数异或为 0 的性质，可以实现状态切换：

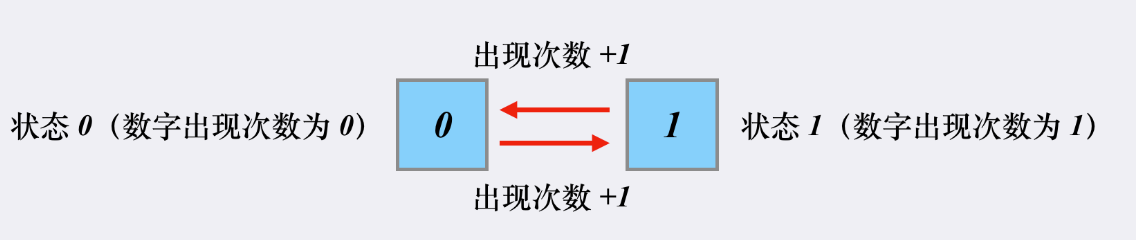
当出现三个的时候，明显是需要标记多一个状态

 

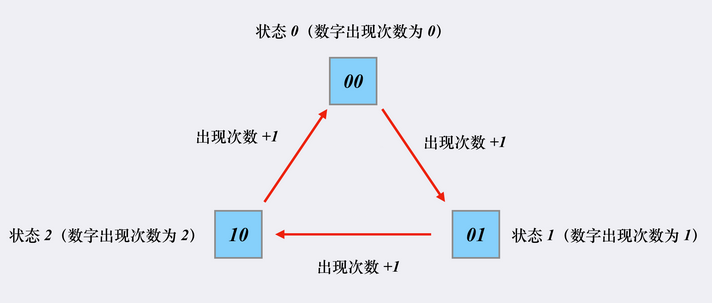
举例子：
以【10,10,10,100】为例
当第一次进入的时候
x = 10,所以 one ^ x 这部分为 10 而 ~two （由于two为0，所以得到-1）
故10&-1 = 10（相当于00001010&11111111 = 00001010）
为什么-1是11111111，要记住存的是补码，所以补码转为原码即：
11111111 - 1 = 11111110 符号位不变，其他变则为 10000001 （这就是-1）
所以后面two ^ x 部分也为10 ，而此时~one （由于上面已经变为了10，故的到-11）
所以10&-11 = 0 （相当于00001010&11110101）

第二次的时候
x = 10，所以 one ^ x 这部分为 10^10 = 0 而 ~two = -1
故0&-1 = 0
所以后面two ^ x 部分也为0^10 = 10 ,此时~one = -1
所以10&-1 = 10

第三次的时候
x = 10，one ^ x 这部分为 0^10 = 10 而 ~two = -11
故0&-1 = 0
所以后面two ^ x 部分也为10^10 = 00 ,此时~one = -1
所以0&-1 = 0

重点理解非运算：
比如：~37
在Java中，int 占四个字节，一个字节占8bit位，就是32位，32bit.
37转为二进制是100101.
计算机保存的都是补码，37是正数，他的原码，反码，补码都是一样的；
37在计算机中的补码：
00000000 00000000 00000000 00100101

~37的计算结果：
第一步：求37在计算中补码的相反码（不是反码），这里还是补码只是相反的补码
11111111 11111111 11111111 11011010
第二步：将相反的补码，转换为原码，由于相反码的第一个位是1，这个数是负数，负数的补码转反码 减一（-1）
11111111 11111111 11111111 11011010 -1
= 
11111111 11111111 11111111 11011001
反码转原码：符号位不变，其他数相反
10000000 00000000 00000000 00100110
二进制100110十进制38
符号位不变-38

代码展示：

DFA的代码：

//时间0 ms击败100%
//内存41.4 MB击败11.19%
//时间复杂度：O(n)
//空间复杂度：O(1)
class Solution {
    public int singleNumber(int[] nums) {
        int one = 0, two = 0;
        for(int x : nums){
            one = one ^ x & ~two;
            two = two ^ x & ~one;
        }
        return one;
    }
}

 

位数统计的代码：

//时间4 ms击败42.45%
//内存41.3 MB击败14.99%
//时间复杂度：O(n)，针对常量的遍历是可以忽略的
//空间复杂度：O(1)，虽然开辟了数组，但是由于是固定不变的就会认为是常量
class Solution {
    public int singleNumber(int[] nums) {
        int[] cnt = new int[32];
        for (int x : nums) {
            for (int i = 0; i < 32; i++) {
                if (((x >> i) & 1) == 1) {
                    cnt[i]++;
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < 32; i++) {
            if ((cnt[i] % 3 & 1) == 1) {
                ans += (1 << i);
            }
        }
        return ans;
    }
}

 

使用哈希辅助空间的代码：

//时间5 ms击败37.21%
//内存41.1 MB击败41.76%
//时间复杂度为O(N)
//空间复杂度为O(N),毕竟使用了辅助空间来记录全部数据的个数
class Solution {
    public int singleNumber(int[] nums) {
        HashMap<Integer, Integer> hashMap = new HashMap<>();
        int count = 0;
        for (int i = 0; i < nums.length; i++){
            count = hashMap.getOrDefault(nums[i],0) + 1;
            hashMap.put(nums[i],count);
        }

        for (Integer key : hashMap.keySet()){
            if (hashMap.get(key) == 1){
                return key;
            }
        }
        return 0;
    }
}