剑指 Offer 30. 包含min函数的栈（155. 最小栈）

题目：

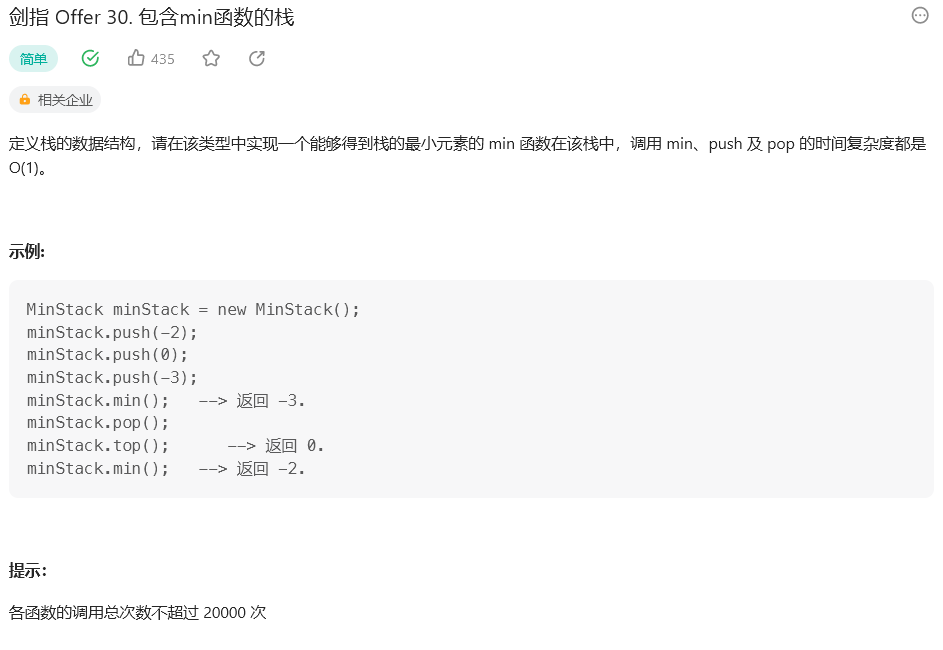
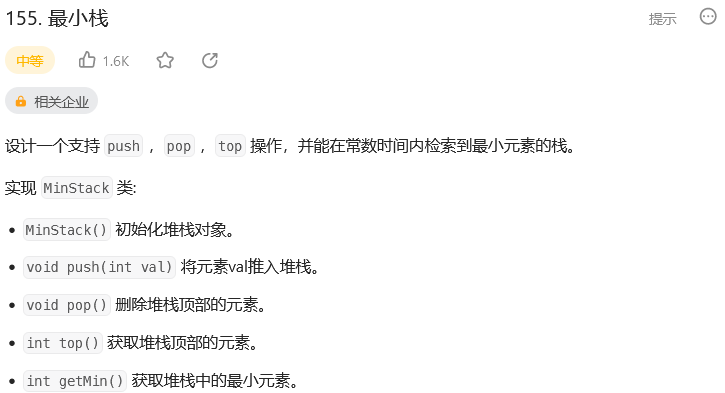
思路：

【1】利用额外空间做记录，保留对应的最小值，这样每次想要获得当前栈的最小值的时候都可以拿到，当然对应元素出栈的时候，对应的最小值也会被抛弃。

时间复杂度：对于题目中的所有操作，时间复杂度均为 O(1)。因为栈的插入、删除与读取操作都是 O(1)，我们定义的每个操作最多调用栈操作两次。
空间复杂度：O(n)，其中 n 为总操作数。最坏情况下，我们会连续插入 n 个元素，此时两个栈占用的空间为 O(n)。

【2】不利用额外空间而是改用差值

代码展示：

利用差值的方式，减少使用额外空间：

//时间12 ms击败98.87%
//内存43.3 MB击败70.73%
//为了防止溢出，采用long替代int
class MinStack {
    Deque<Long> stack;
    long  min;

    public MinStack() {
        stack = new LinkedList<Long>();
    }

    public void push(int x) {
        if (stack.isEmpty()) {
            stack.push(0L);
            min = x;
        } else {
            //这里入栈的是入栈的值和最小值的差值，有可能为负，也有可能为正。
            stack.push(x - min);
            if (x < min){
                min = x;
            }
        }
    }

    public void pop() {
        if (stack.isEmpty()){
            return;
        }
        long  pop = stack.pop();
        //因为入栈的是差值，当出栈的为负数的时候，说明栈中最小值已经出栈了，
        //这里要重新更新最小值
        if (pop < 0){
            min -= pop;
        }
    }

    public int top() {
        long  top = stack.peek();
        if (top > 0) {
            //栈顶元素如果是正的，说明栈顶元素压栈的时候是比栈中最小值大的，根据
            //top=x - min，可以计算x=top+min
            return (int) (top + min);

        } else {
            //当栈顶元素是负数的时候，说明栈顶元素压栈的时候是比栈中最小值小的，
            //而压栈完之后他会更新最小值min，所以如果在使用上面公式肯定是不行
            //的。如果栈顶元素压栈的时候比最小值小，他会更新最小值，这个最小值
            //就是我们要压栈的值，所以这里直接返回min就行了。
            return (int) (min);

        }
    }

    public int min() {
        return (int) (min);
    }
}

 

利用额外空间做记录：

//时间13 ms击败64.36%
//内存43.2 MB击败83.13%
//利用额外的辅助栈空间每个元素对应的最小元素都会被记录下来
class MinStack {
    Deque<Integer> xStack;
    Deque<Integer> minStack;

    public MinStack() {
        xStack = new LinkedList<Integer>();
        minStack = new LinkedList<Integer>();
        minStack.push(Integer.MAX_VALUE);
    }
    
    public void push(int x) {
        xStack.push(x);
        minStack.push(Math.min(minStack.peek(), x));
    }
    
    public void pop() {
        xStack.pop();
        minStack.pop();
    }
    
    public int top() {
        return xStack.peek();
    }
    
    public int min() {
        return minStack.peek();
    }
}