矩阵置零（73. 矩阵置零）

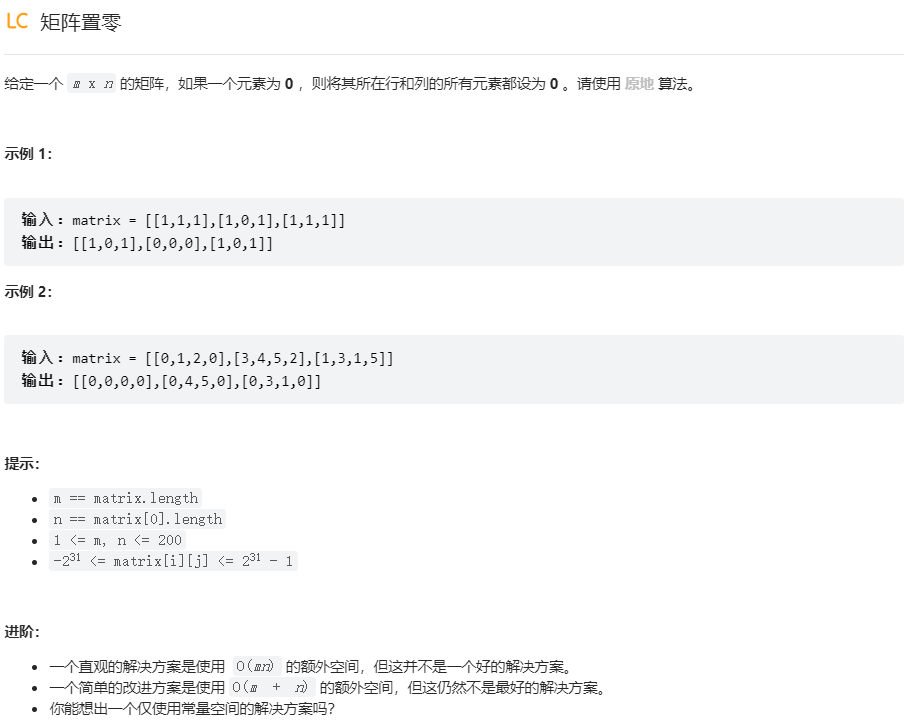
题目：

思路：

【1】首先简单点，考虑使用辅助空间，然后对于数组肯定是要遍历的，时间复杂度是O(N^2)，遍历第一次肯定要标记一下哪一行与哪一列是要变为0的。然后开始第二次循环，根据标记置为0。思路看着颇为清新。

【2】对于进阶要求使用常量空间，其实本质上可以采用数组的第一行与第一列进行替代：

第一行与第一列没有0的情况：
[3,4,5,2]
[3,0,2,0]
[1,3,1,5]
这种情况最为简单：
因为行与列都应该从下标为1开始遍历，遇到为0的就将对应的第一行与第一列的数值置为0：
[3,0,5,0]
[0,0,2,0]
[1,3,1,5]
然后再次遍历，根据第一行与第一列的数值是否为零进行判断：
[3,0,5,0]
[0,0,0,0]
[1,0,1,0]
又由于第一行和第一列没有0，所以不需要再做处理

但如果是第一行和第一列有0的情况，即：
[0,4,5,2]
[3,0,2,0]
[1,3,1,5]
前面的与上面没多大差距，直到
[0,0,5,0]
[0,0,0,0]
[1,0,1,0]
这时候由于第一行和第一列有0，所以需要处理：
第一行有0，将第一行全部置为0：
[0,0,0,0]
[0,0,0,0]
[1,0,1,0]
第一列有0，将第一列全部置为0：
[0,0,0,0]
[0,0,0,0]
[0,0,1,0]
完成处理

代码展示：

利用M+N的辅助空间处理：

//执行用时：1 ms, 在所有 Java 提交中击败了37.88%的用户
//内存消耗：43.2 MB, 在所有 Java 提交中击败了36.59%的用户
class Solution {
    public void setZeroes(int[][] matrix) {
        //行
        int m = matrix.length;
        //列
        int n = matrix[0].length;
        boolean[] zeros = new boolean[m+n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if(matrix[i][j] == 0){
                    // 将行信息为0的存放在数组【0-m】下标
                    zeros[i] = true;
                    // 将列信息为0的存放在数组【m-m+n】下标
                    zeros[m+j] = true;
                }
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 该行有0，将该元素置0
                if(zeros[i]){
                    matrix[i][j] = 0;
                }
                // 改列有0.该元素置0
                if(zeros[j+m]){
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

常量空间的方式【本质上就是拿数组的第一行与第一列来替代上面的辅助空间】【这种相比于上面的话可能出现少遍历第一行和第一列的情况，而且下面还不是最优的，因为为了写简便还是采用了双循环，正确的应该采用单循环，遍历第一行与第一列，如果没有0，则跳过，这样又能减少遍历次数，但是时间复杂度没有变化，因为还是需要遍历全部查找0】：

//执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗：42.9 MB, 在所有 Java 提交中击败了62.99%的用户
class Solution {
    public void setZeroes(int[][] matrix) {
        //标记第一行是否有数字0
        boolean row = false;
        //标记第一列是否有数字0
        boolean col = false;
        //遍历第一列
        for (int[] ints : matrix) {
            if (ints[0] == 0) {
                col = true;
                break;
            }
        }
        //遍历第一行
        for (int i = 0; i < matrix[0].length; i++) {
            if (matrix[0][i] == 0) {
                row = true;
                break;
            }
        }
        for (int i = 1; i < matrix.length; i++) {
            for (int j = 1; j < matrix[0].length; j++) {
                if(matrix[i][j] == 0){
                    // 将行信息为0的存放在数组第一列中
                    matrix[i][0] = 0;
                    // 将列信息为0的存放在数组第一行中
                    matrix[0][j] = 0;
                }
            }
        }
        //开始填充数据
        for (int i = 1; i < matrix.length; i++) {
            for (int j = 1; j < matrix[0].length; j++) {
                // 根据第一行和第一列判断该数是否应该被置为0
                if(matrix[i][0] == 0 || matrix[0][j] == 0){
                    matrix[i][j] = 0;
                }
            }
        }
        //判断第一列是否需要填充
        if(col) {
            for (int i = 0; i < matrix.length; i++) {
                matrix[i][0] = 0;
            }
        }
        //判断第一行是否需要填充
        if(row) {
            for (int i = 0; i < matrix[0].length; i++) {
                matrix[0][i] = 0;
            }
        }
    }
}