两整数之和（剑指 Offer 65. 不用加减乘除做加法）

题目：

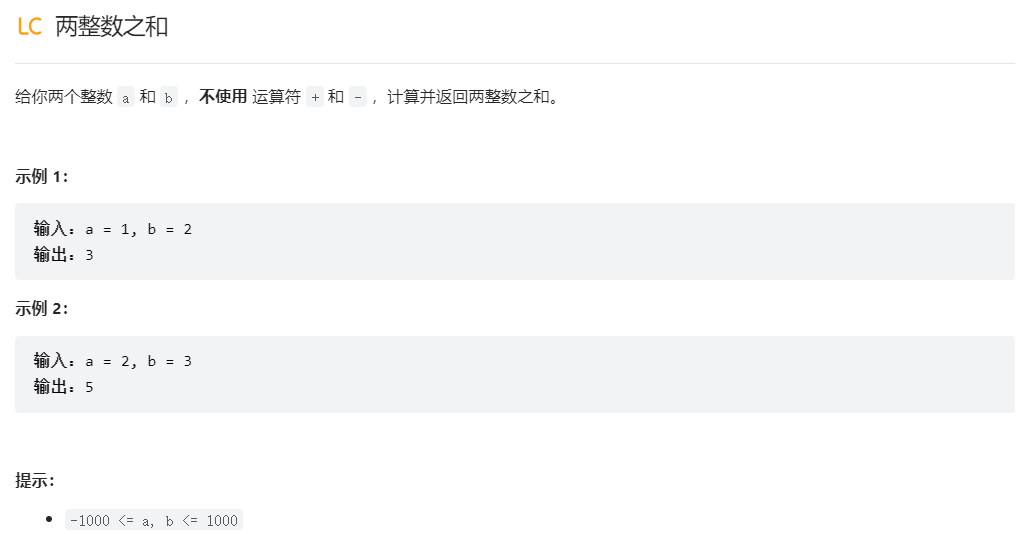
思路：

【1】这两道题本质上考察的是差不多的意思。

【2】这道题的本质上是考察二进制，因为在编程中数据是采用二进制进行存储的，所以便是要考察二进制的处理，即异或(^),相与(&)

理解异或 和 相与
异或： 当 1与1进行异或的时候得0,0与1异或的时候得1
相与： 当 1与1进行相与的时候得1,0与1相与的时候得0，0与0相与的时候得0

先分析 3+5 【这里采用的是tinyint来解释【可容纳-128~127，或无符号的0~255】，只有1字节（Bety），即8位（bit】：
3用二进制表示为00000011
5用二进制表示为00000101

那怎么表示3+5呢
先3^5【这里是全体异或哦，新手别懵】：
00000011^00000101=00000110=6
得出6明显还不是最终结果【因为只是将一部分像加到了一起】
此时还要处理进位问题
则3&5：
00000011&00000101=00000001=1
因为这部分是两者都有的，所以相加到一起的话是需要进位的，那怎么进位呢？
x=3&5
x<<1【即采用位移，向左移动一位】
x<<1 = 00000010 = 2

此时重复步骤【即现在变为了6+2】
最终得到【8+0】即为结束

接下来分析3-5，可以看作为【3+（-5）】,
这需要了解一下概念
在Java/C++中正数和负数的存储方式
正数是以正码的形式存储
负数是以补码的形式存储

说明：
正码就是一个数的真实值，如00000011代表了1*（2^1）+1*（2^0）
而反码：就是正码取反，即11111100
而补码：就是反码加1，即11111101

那么3-5：
开始第一次
先x1=3^-5：
00000011^11111011=11111000
则y1=3&-5：
00000011&11111011=00000011
接着y1 = y1<<1 = 00000110

重复第二次：
先x2 = x1^y1
11111000^00000110=11111110
在y2 = x1&y1
11111000&00000110=00000000
最后y2 = y2<<1 = 00000000

代码展示：

采用异或运算的方案：

限制可以用变量个数的话，可以改为这样：

c=a&b;
a=a^b;
b=c<<1;
不限制的话下面这种会比较好看一点

class Solution {
    public int getSum(int a, int b) {
        int x,y;
        while (b!=0){
            x=a;
            y=b;
            a = x^y;
            b = (x&y)<<1;
        }
        return a;
    }
}