剑指 Offer 16. 数值的整数次方（50. Pow(x, n)）

题目：

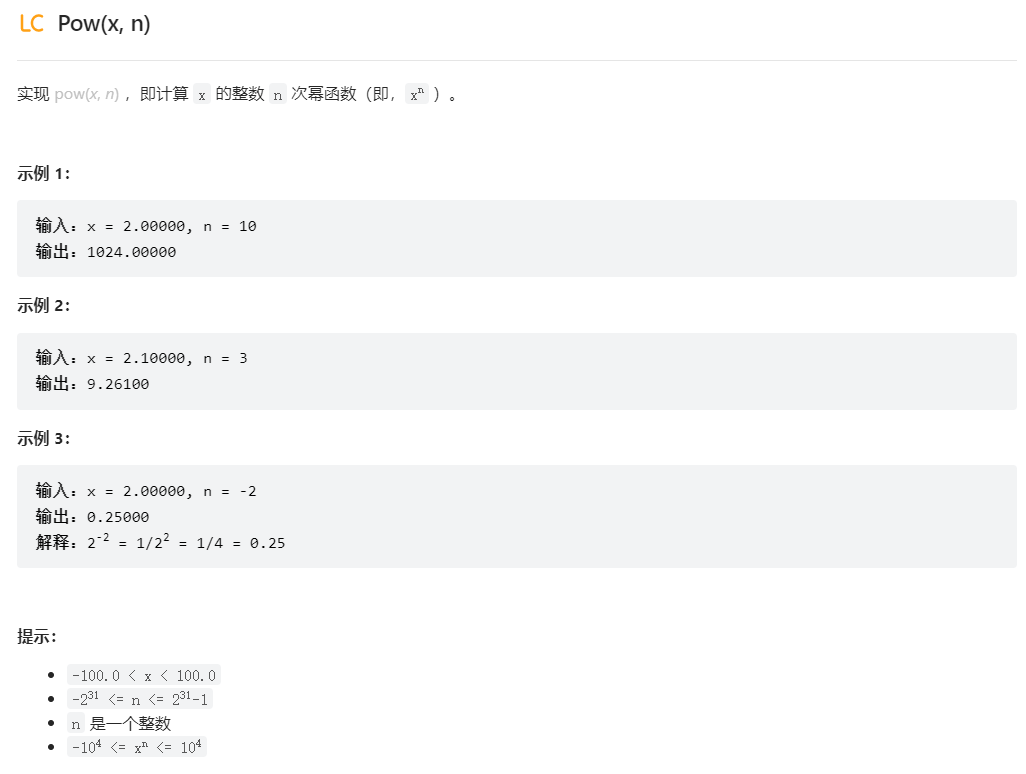
思路：

【1】首先必然是按照规律顺序写出来，那么就是暴力破解思维，采用单循环来处理，但是基于n可以达到int的最大范围值，这个时候会容易变成遍历很多的情况，又由于在数学是2的16次方 其实与 4的八次方，8的4次方，16的2次方是相等的，那么基于这种思路可以将16次循环减少为3次【折半思维】。

代码展示：

基于暴力破解写的：

首先是是次方数，本身就X*X这个不用多管，其次就会是n会为负数，那么这个就要处理一下，也就是x要变为1/x。

但是这种面对x = 0.00001, n = 2147483647时会超时，因为要遍历的次数太多了

class Solution {
    public double myPow(double x, int n) {
        //为了暴力思维能过，进行特殊处理
        if( n<=-2147483647 || n==2147483647){
            if (n % 2 == 0 && x<0){
                x = -x;
            }
            return x == 1 || x == -1 ? x:0;
        }
        
        double res = 1.0;
        for (int i = n; i != 0; i--) {
            if (i<0){
                i = -i;
            }
            res *= x;
        }
        return n < 0 ? 1 / res : res;
    }
}

 

基于折半思维的代码：

//时间0 ms 击败 100%
//内存40.5 MB 击败 67.64%
class Solution {
    public double myPow(double x, int n) {
        //过程展示
        //数据示例： 计算 x = 2 的整数 i = 5 次幂
        //结果先设置为 res = 1;
        //此时的 幂数i 为：5  由于是奇数 所以抽一个出来
        //即 res = res * x ，将 x 变为 x^2
        //此时的 幂数i 为：2 , 相当于 (x^2)^2,再倍增 x = x*x
        //此时的 幂数i 为：1 ， 相当于 (x^4) ，由于是奇数，所以
        //即 res = res * x * (x^4)
        double res = 1.0;
        for (int i = n; i != 0; i /= 2) {
            if (i % 2 != 0) {
                res *= x;
            }
            x *= x;
        }
        return n < 0 ? 1 / res : res;
    }
}