阶乘后的零（172. 阶乘后的零）

题目：

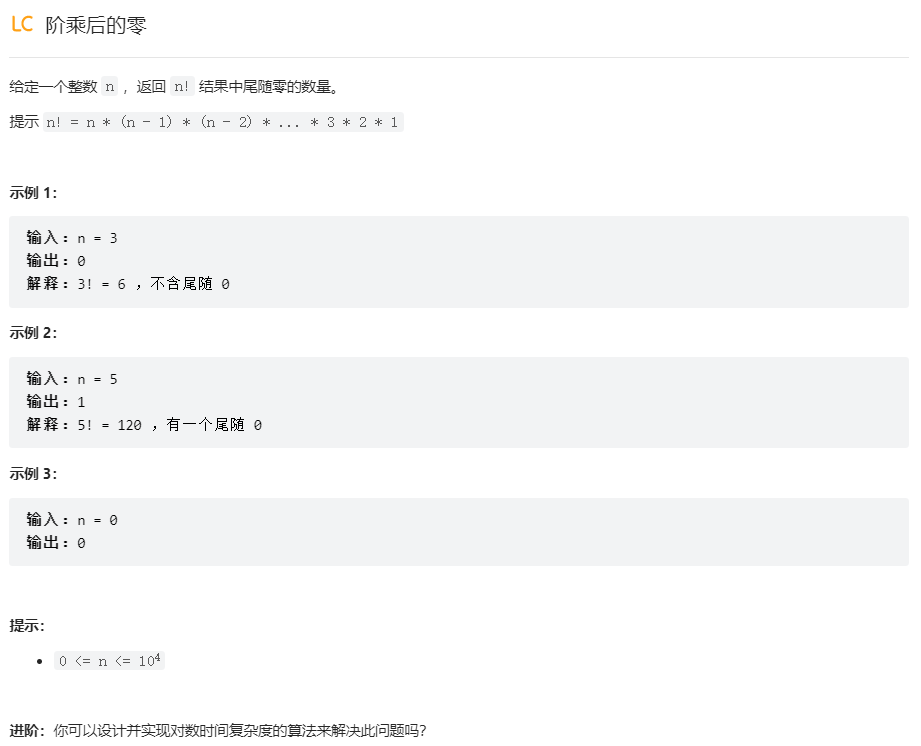
思路：

【1】正常点的思维大概率会是先阶乘把数算出来，然后转成字符串遍历0的个数，但是这样很容易超出类型的限制范围，所以只能推导数学公式，首先0的产生必然是10乘以某个数，而10的产生必然是2*5【要记住是尾随的0，所以必然是10导致的】。

而且在阶乘里面，如5！或10！
分解：
5！=5*4*3*2*1=5*（2*2）*3*2*1；
10！=10*9*8*7*6*5*4*3*2*1=（2*5）*（3*3）*（2*2*2）*7*（2*3）*5*（2*2）*3*2*1；
可以看出2的个数必然是比5要多的。
所以基本算出5的个数就是尾随的0的个数。

而
含有5的有【只列出一百以内的】
5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100
所以
因为是阶乘，正常可以根据遍历，限制步长为5计算里面的5的个数，便可以得到0的个数

但是对于进阶要求的是对数，那么其实就是要求用除法，所以可以考虑怎么用除法得出5的个数
当在小于50的时候
如24，含有5的便是【5,10,15,20】
进行分解【1*5,2*5,3*5,4*5】
含有4个5，等同于24/5=4，余数为4

如25，含有5的便是【5,10,15,20,25】
进行分解【1*5,2*5,3*5,4*5,5*5】
含有6个5，而25/5=5，余数为0
那么基于商在进行除一遍的5/5=1，加起来便可以等于6

那么对其他数进行验证：
如49，含有5的便是【5,10,15,20,25,30,35,40,45】，
进行分解【1*5,2*5,3*5,4*5,5*5,6*5,7*5,8*5,9*5】，
含有10个5
所以49/5=9,9/5=1，加起来刚好等于10

那么对于50呢，他存在12个5
含有5的便是【5,10,15,20,25,30,35,40,45。50】，
进行分解【1*5,2*5,3*5,4*5,5*5,6*5,7*5,8*5,9*5,2*5*5】，
50/5=10,10/5=2,刚好也满足

故，n/5=k，如果k>5,则进行重复步骤，然后将结果累加便是答案

 

代码展示：

采用循环遍历的方式：

class Solution {
    public int trailingZeroes(int n) {
        int ans = 0;
        for (int i = 5; i <= n; i += 5) {
            int temp = i;
            //这一步可以看做为一个整体，因为只是为了求出5的个数
            while (temp % 5 == 0) {
                ans++;
                temp /= 5;
            }
        }

        return ans;
    }
}

 

正常数学逻辑的方案代码【这种只用了一个循环，且除以的是5，其实便是对数的时间复杂度了，时间复杂度为O（logN）】：

class Solution {
    public int trailingZeroes(int n) {
        int count = 0;
        while (n >= 5){
            //每次得出该次的前缀表示该次的次数。
            count += n/5;
            n /= 5;
        }
        return count;
    }
}

当然更进一步基于限制n最大就是10000的情况还可以这样【这种是直接把5的倍数列出来，并且是在限制内的，所示基于上面的符合当前题目的写法，但是限制扩大了就会变得不合适，好处就是时间复杂度直接会降为O（1）】：

class Solution {
    public int trailingZeroes(int n) {
        return n/5+n/25+n/125+n/625+n/3125;
    }
}