x 的平方根

题目：

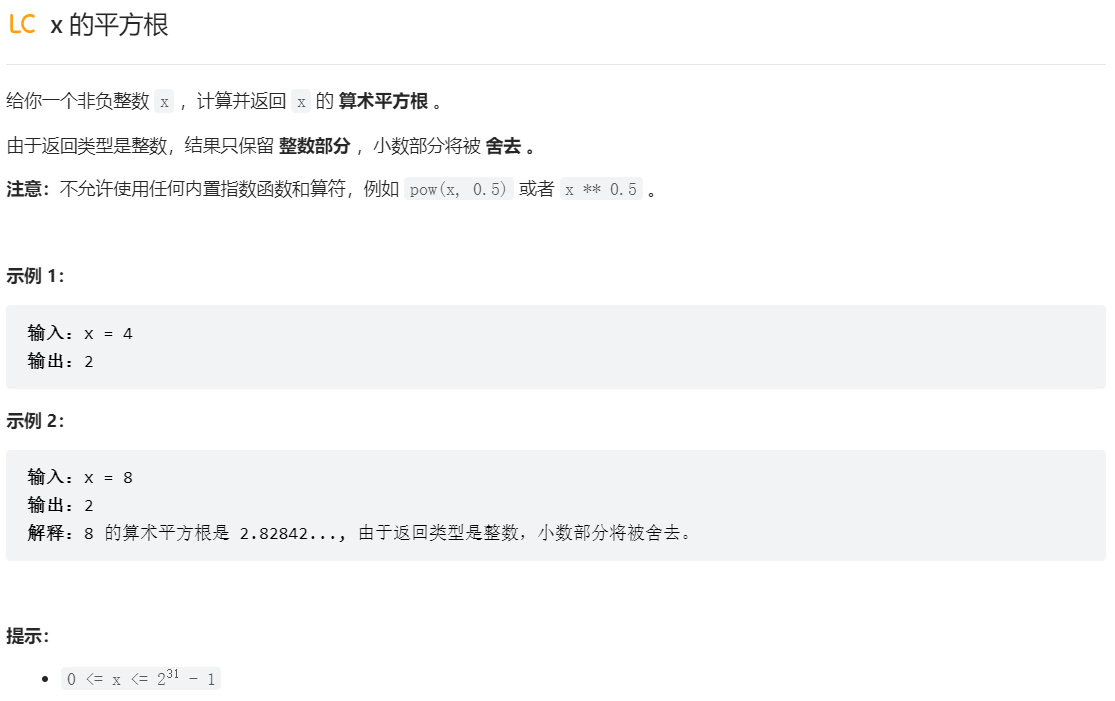
思路：

【1】话不多说这道题本身暴力破解是可以过的，而且基于限制为Integer.MAX_VALUE，所以可以知道根号为46341，那么基于这个进行遍历就好了。

【2】基于二分进行优化，因为从暴力破解这里我们看到了，不一定需要遍历那么多数据，所以筛选数据快的方式不就是二分吗，一下子过掉一半的数据。

代码展示：

暴力破解：

//执行用时：20 ms, 在所有 Java 提交中击败了9.73%的用户
//内存消耗：38.6 MB, 在所有 Java 提交中击败了83.56%的用户
//由于System.out.println(Math.sqrt(Integer.MAX_VALUE));  ----> 46340.950001051984
class Solution {
    public int mySqrt(int x) {
        //其次如果是0和1其实直接返回就好了
        if (x == 0 || x == 1) {
            return x;
        }
        //因为遍历到了便会终止所以不需要在意46341
        for (int i = 1; i < 46341 ; i++) {
            if (i * i > x) {
                return i - 1;
            }
        }
        //如果到了这里基本x就是Integer.MAX_VALUE
        return 46340;
    }
}

 

常规的二分优化处理：

//执行用时：1 ms, 在所有 Java 提交中击败了93.76%的用户
//内存消耗：38.4 MB, 在所有 Java 提交中击败了95.73%的用户
class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

//执行用时：1 ms, 在所有 Java 提交中击败了93.76%的用户
//内存消耗：38.6 MB, 在所有 Java 提交中击败了75.42%的用户
class Solution {
    public int mySqrt(int x) {
        if (x == 1 ){
            return 1;
        }
        int l = 0, r = x/2, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

当然如果只是想刷题的话，推荐【毕竟内置函数耗时最短】：

//执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗：38.8 MB, 在所有 Java 提交中击败了54.18%的用户
class Solution {
    public int mySqrt(int x) {
        return (int)Math.sqrt(x);
    }
}

 

Integer.MAX_VALUE