剑指 Offer 56. 数组中数字出现的次数

题目：

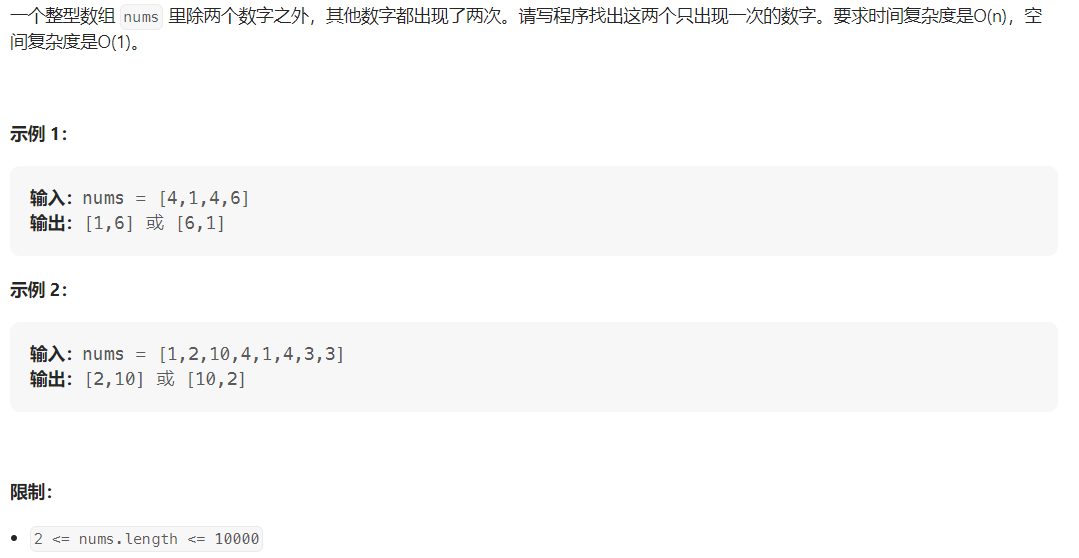
【1】第一种

 

 

 

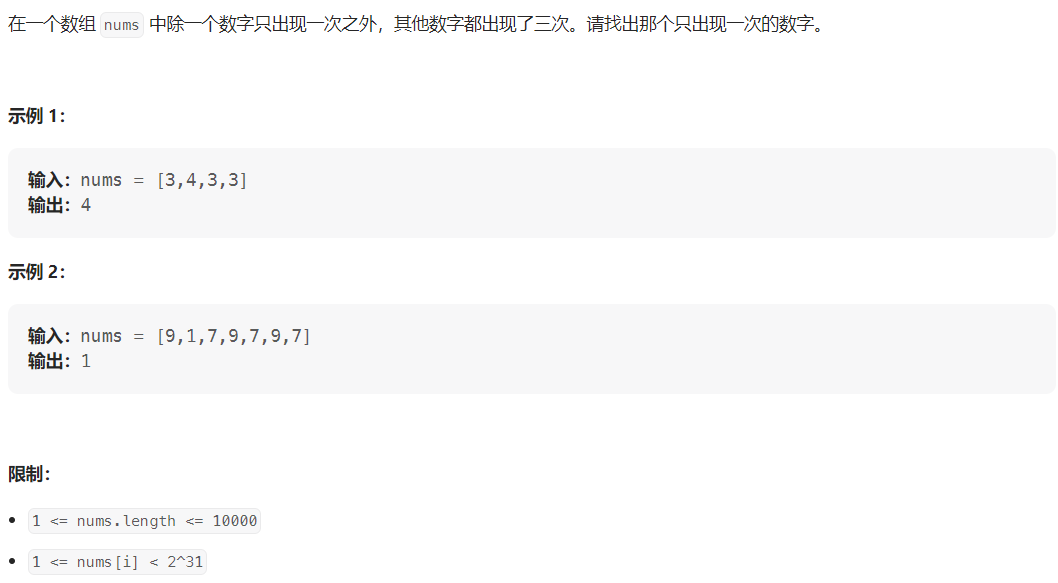
【2】第二种

 

 

 

思路：

【1】第一种，考察的是位运算，因为限制了不能使用数组的存储空间，也限制对双循环的使用。但是基于异或的特性，相同的数值相异得到0，所以是可以得到一个唯一的数值的，但是这里面是两个，所以就需要考察如何将这两个进行分割开来。

【2】第二种，这种较第一种限制不多，暴力破解，使用辅助空间都能做，区别是在于性能。

代码展示：

//剑指 Offer 56. 数组中数字出现的次数
public class Offer {
    public static void main(String[] args) {
        int[] arr = new int[]{3,4,3,3};

        System.out.println(Method3(arr));
    }

    //第一种情况，要求时间复杂度是O(n)，空间复杂度是O(1)
    //那边说明了限制不能使用双循环，其次不能开辟数组空间
    //而且还是两个数字只出现一次
    public static int[] Method1(int[] nums){
        //将所有的数异或起来
        int k = 0;
        //由于是两个数，所以异或完后存在这个数中的1便是两个数不同的地方
        //如假设这两个数为a，b，如果a的二进制第5位为1，而b的第五位为0，那么k的第五位就会为1
        for(int num: nums) {
            k ^= num;
        }
        //那么便找出，最小的不同位
        int diff = 1;
        while((k & diff) == 0) {
            diff <<= 1;
        }

        int a = 0;
        int b = 0;
        //根据最小的不同位来区别两个数字
        for(int num: nums) {
            if((num & diff) == 0) {
                a ^= num;
            } else {
                b ^= num;
            }
        }

        return new int[]{a, b};
    }

    //第二种情况，这种便是固定统计位数的个数
    //由于1 <= nums.length <= 10000，所以如果是要存储hashMap来记录出现的个数，那么最多会出现要存三千多个的情况
    //但是通过记录位数出现的次数，则需要记录固定的32个位数
    //然后通过根据对应出现次数来取余数，则会得出最终位数应该是多少，再汇总得出数字
    //时间 3 ms 击败 85.39%
    //内存 42.3 MB 击败 80.40%
    //时间复杂度 O(N) ： 其中 N 位数组 nums 的长度；遍历数组占用 O(N) ，每轮中的常数个位运算操作占用 O(1) 。
    //空间复杂度 O(1)： 数组 counts长度恒为 323232 ，占用常数大小的额外空间
    public static int Method2(int[] nums){
        int[] counts = new int[32];
        for(int num : nums) {
            for(int j = 0; j < 32; j++) {
                counts[j] += num & 1;
                num >>>= 1;
            }
        }
        int res = 0, m = 3;
        for(int i = 0; i < 32; i++) {
            res <<= 1;
            res |= counts[31 - i] % m;
        }
        return res;
    }

    //第二种情况，利用异或来进行处理
　　// 对于整数 num，当 num 出现一次至三次时，对应的 ones 和 twos 分别如下。
　　//当 num 出现一次时，ones=num ，twos=0。
　　//当 num 出现两次时，ones=0，twos=num。
　　//当 num 出现三次时，ones=0，twos=0。
　　//时间复杂度 O(N) ： 其中 N 位数组 nums 的长度；遍历数组占用 O(N) ，每轮中的常数个位运算操作占用 O(32×3×2)=O(1)。
　　//空间复杂度 O(1) ： 变量 ones , twos 使用常数大小的额外空间。
　　//假设nums为{3,4,3,3}，~twos即对数字进行取反,0变1，1变0
　　// 当twos = 0时，~twos就是-1，二进制即111111111
　　// 当twos = 1时，~twos就是-2，二进制即111111110
//第一次循环：参数3
//      ones = 0000 ^ 0011 & 111111111  得ones=0011
//      twos = 0000 ^ 0011 & 111111100  得twos=0000
//第二次循环：参数4
//      ones = 0011 ^ 0100 & 111111111  得ones=0111
//      twos = 0000 ^ 0100 & 111111000  得twos=0000
//第三次循环：参数3
//      ones = 0111 ^ 0011 & 111111111  得ones=0100
//      twos = 0000 ^ 0011 & 111111011  得twos=0011
//第四次循环：参数3
//      ones = 0100 ^ 0011 & 111111100  得ones=0100
//      twos = 0000 ^ 0011 & 111111000  得twos=0000
    public static int Method3(int[] nums){
        int ones = 0, twos = 0;

        for(int num : nums){
            ones = ones ^ num & ~twos;
            twos = twos ^ num & ~ones;
        }
        return ones;
    }
}