剑指 Offer 14. 剪绳子（343. 整数拆分）

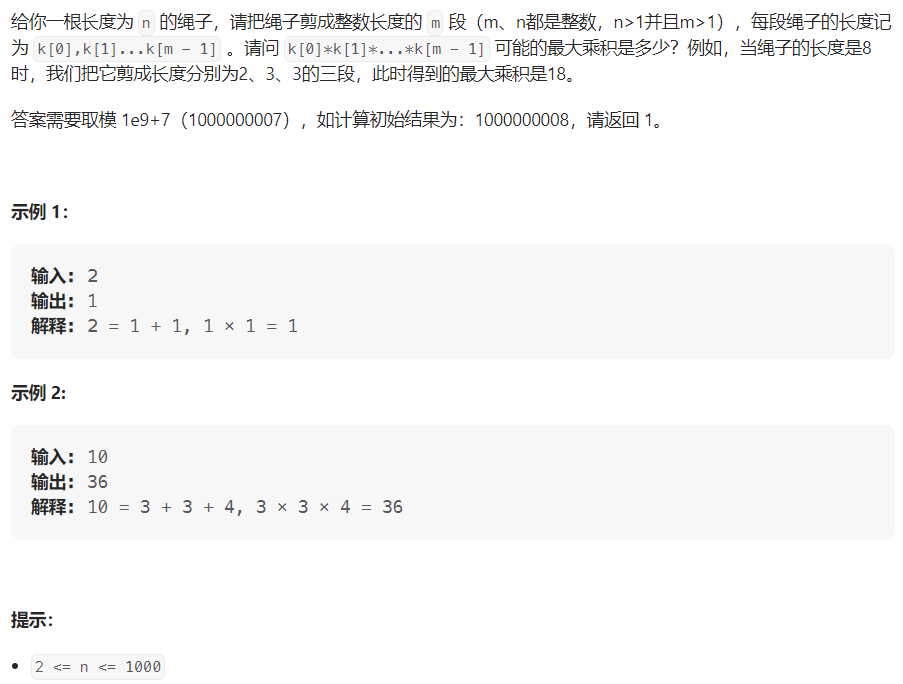
题目：

【1】第一种【这种算是比较常规的，主要考察的是切分的思维】

 

 

【2】第二种【这是第一种的变种，考察的是对数据类型范围的处理，因为int的范围不足以容纳下结果】

 

 

思路：

【1】思路一：贪心算法，贪心算法是要经过数学推到得出最优值，如在计算乘积最大的时候，会发现优先长度是3的，乘积是最大的，所以就需要优先分长度为3。其次还会有一些特殊情况，如4,3,2。因为条件里面是必须剪一刀，故要进行特殊处理。

【2】思路二：动态规划，也就是一步步的推上去，从绳子长度为1，推到绳子长度为n的最大乘积。

【3】针对变种的情况更多的是考虑到对数据容量的思考，因为当容量变大了，其实int是不合适的，贪心的情况可以考虑long类型，然后取余强转换，但是对于动态规划显然是不行的，因为存在一层层的往上推，大数相乘很容易就会溢出long类型的范围，所以要采用BigInteger类型。

代码展示：

public class Offer {
    public static void main(String[] args) {
        Random random = new Random();
        int target = random.nextInt(57)+2;
        System.out.println(Method4(120));
    }


    //思路一：贪心算法
    // 基于m>1，所以表明了至少要剪一刀
    public static int Method1(int n){
        //由于n>1，所以不考虑绳子长度为1的情况，考虑2返回1，3返回2，因为必须剪一下
        if (n <= 3){
            return n-1;
        }
        if (n == 4){
            return 4;
        }
        int result = 1;
        while (n > 4){
            result *= 3;
            n -= 3;
        }
        //因为按3剪最后可能会剩下2或1,2要补上
        return result*n;
    }

    //在变种的情况下，也就是将输入值的范围扩大为 2 <= n <= 1000
    //而int: 32位整数 -2,147,483,648——2,147,483,647
    //long: 64位整数 -9,223,372,036,854,775,808—— 9,223,372,036,854,775,807
    public static int Method2(int n){
        //由于n>1，所以不考虑绳子长度为1的情况，考虑2返回1，3返回2，因为必须剪一下
        if (n <= 3){
            return n-1;
        }
        if (n == 4){
            return 4;
        }
        //所以存在溢出的情况下就只能用long了
        long result = 1;
        long limit = 1000000007;
        while (n > 4){
            result = result*3%limit;
            n -= 3;
        }

        //因为按3剪最后可能会剩下2或1,2要补上，且要转回为int
        return (int)(result*n%limit);
    }
    //思路二：动态规划
    public static int Method3(int n){
        if (n <= 3){
            return n-1;
        }
        if (n == 4){
            return 4;
        }
        int[] dp = new int[n+1];
        //至于这里为什么是1，2，3？是因为这里是剪掉的部分的最大值，如5剪成2*3，那么3的部分最大值是3，因为3在不剪的情况下大于剪之后的，2也同理。
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;
        for (int i = 4; i<=n;i++){
            //j<=i/2是因为1*3和3*1是一样的，没必要计算在内，只要计算到1*3和2*2就好了【减少计算量】
            for (int j = 1;j<= i/2;j++){
                //max(j*(i-j),j*dp[i-j]是由于减去第一段长度为j的绳子后，可以继续剪也可以不剪
                //如果不剪就是j*(i-j)，如果继续剪那么dp[i-j]就是这部分的剪得效果的最大值
                //max(dp[i],Math.max(j*(i-j),j*dp[i-j]))是当j不同时，求出最大的dp[i]
                dp[i] = Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
            }
        }
        return dp[n];
    }

    //针对变种情况，动态规划其实变动不用很大，就是将类型改一下
    //但是你会发现int和long其实都会存在溢出的问题，所以改用BigInteger
    public static int Method4(int n){
        if (n <= 3){
            return n-1;
        }
        if (n == 4){
            return 4;
        }
        BigInteger dp[] = new BigInteger[n + 1];
        Arrays.fill(dp, BigInteger.valueOf(1));
        //至于这里为什么是1，2，3？是因为这里是剪掉的部分的最大值，如5剪成2*3，那么3的部分最大值是3，因为3在不剪的情况下大于剪之后的，2也同理。
        dp[2] = BigInteger.valueOf(2);
        dp[3] = BigInteger.valueOf(3);
        for (int i = 4; i<=n;i++){
            //j<=i/2是因为1*3和3*1是一样的，没必要计算在内，只要计算到1*3和2*2就好了【减少计算量】
            for (int j = 1;j<= i/2;j++){
                //max(j*(i-j),j*dp[i-j]是由于减去第一段长度为j的绳子后，可以继续剪也可以不剪
                //如果不剪就是j*(i-j)，如果继续剪那么dp[i-j]就是这部分的剪得效果的最大值
                //max(dp[i],Math.max(j*(i-j),j*dp[i-j]))是当j不同时，求出最大的dp[i]
                dp[i] = dp[i].max(BigInteger.valueOf(j * (i - j))).max(dp[i - j].multiply(BigInteger.valueOf(j)));

            }
        }
        return  dp[n].mod(BigInteger.valueOf(1000000007)).intValue();
    }
}