剑指 Offer 07. 重建二叉树（105. 从前序与中序遍历序列构造二叉树）

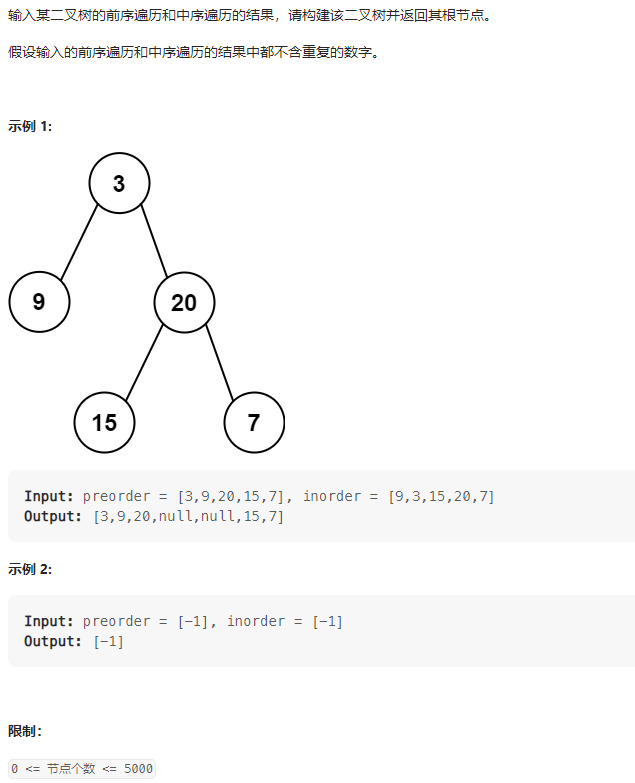
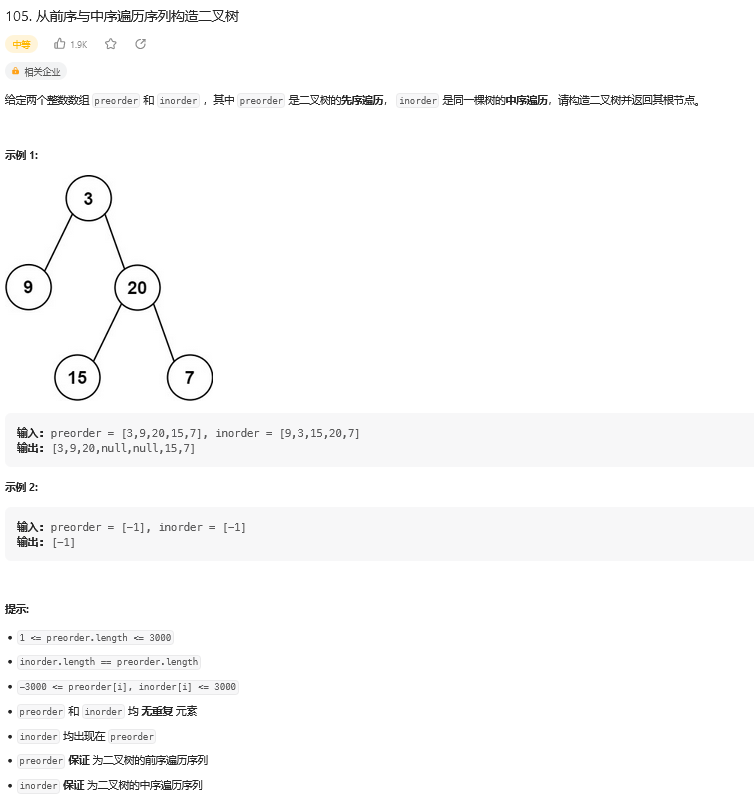
题目：

思路：

【1】利用递归的方式【这种其实是最好理解的】

对于任意一颗树而言，前序遍历的形式总是【根节点总是前序遍历中的第一个节点】：
[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

中序遍历的形式总是：
[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

那么基于这种方式转换一下，不就是可以对每一个子树都一样这样分解吗？

 

【2】利用循环来替代递归的方式

代码展示：

利用循环来替代递归的方式：

//时间1 ms击败99.10%
//内存41 MB击败78.44%
//时间复杂度：O(n)，其中 n 是树中的节点个数。
//空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，我们还需要使用 O(h)（其中 h 是树的高度）的空间存储栈。
//这里 h<n，所以（在最坏情况下）总空间复杂度为 O(n)。
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || preorder.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[0]);
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        stack.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < preorder.length; i++) {
            int preorderVal = preorder[i];
            TreeNode node = stack.peek();
            if (node.val != inorder[inorderIndex]) {
                node.left = new TreeNode(preorderVal);
                stack.push(node.left);
            } else {
                while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
                    node = stack.pop();
                    inorderIndex++;
                }
                node.right = new TreeNode(preorderVal);
                stack.push(node.right);
            }
        }
        return root;
    }
}

 

利用递归的方式：

//时间1 ms击败99.10%
//内存40.8 MB击败97.86%
//时间复杂度：O(n)，其中 n 是树中的节点个数。
//空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，我们还需要使用 O(n) 的空间存储哈希映射，以及 O(h)（其中 h 是树的高度）的空间表示递归时栈空间。这里 h<n，所以总空间复杂度为 O(n)。
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<Integer, Integer> indexMap;

    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right)  return null;

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);
        
        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
}