剑指 Offer 04. 二维数组中的查找

题目：

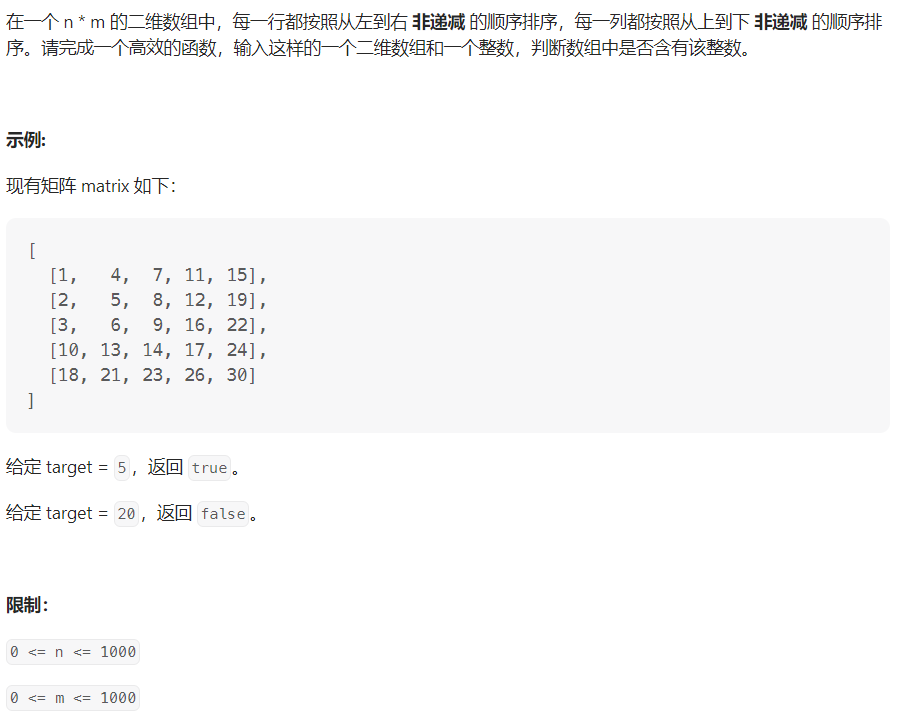
思路：

【1】思路一：毫无头绪之下，其实暴力破解，采用双循环也是不错的，毕竟做出来总比没做出来的要好。

【2】思路二：一看到有序，其实可以考虑二分查找，基于暴力破解的基础上，对每一行的遍历采用二分查找来进行优化减少遍历次数。【但是其实还是不够优化】

【3】思路三：其实有考虑过对角线，进行二分查找，但是对角线会存在一个问题，其实就是只能筛选出部分数据，如数据示例：

//每一行的数据
参数：[1, 10, 16, 26, 27, 34]
参数：[8, 13, 26, 32, 41, 42]
参数：[17, 25, 29, 35, 44, 46]
参数：[20, 33, 38, 47, 49, 50]
参数：[23, 39, 40, 50, 54, 58]
参数target：42

【4】思路四：而是二分查找，不过是基于他这种结构和图十分相像，可以按图的方式进行遍历，次数最少，而且不用开辟过多的空间。如图：

 

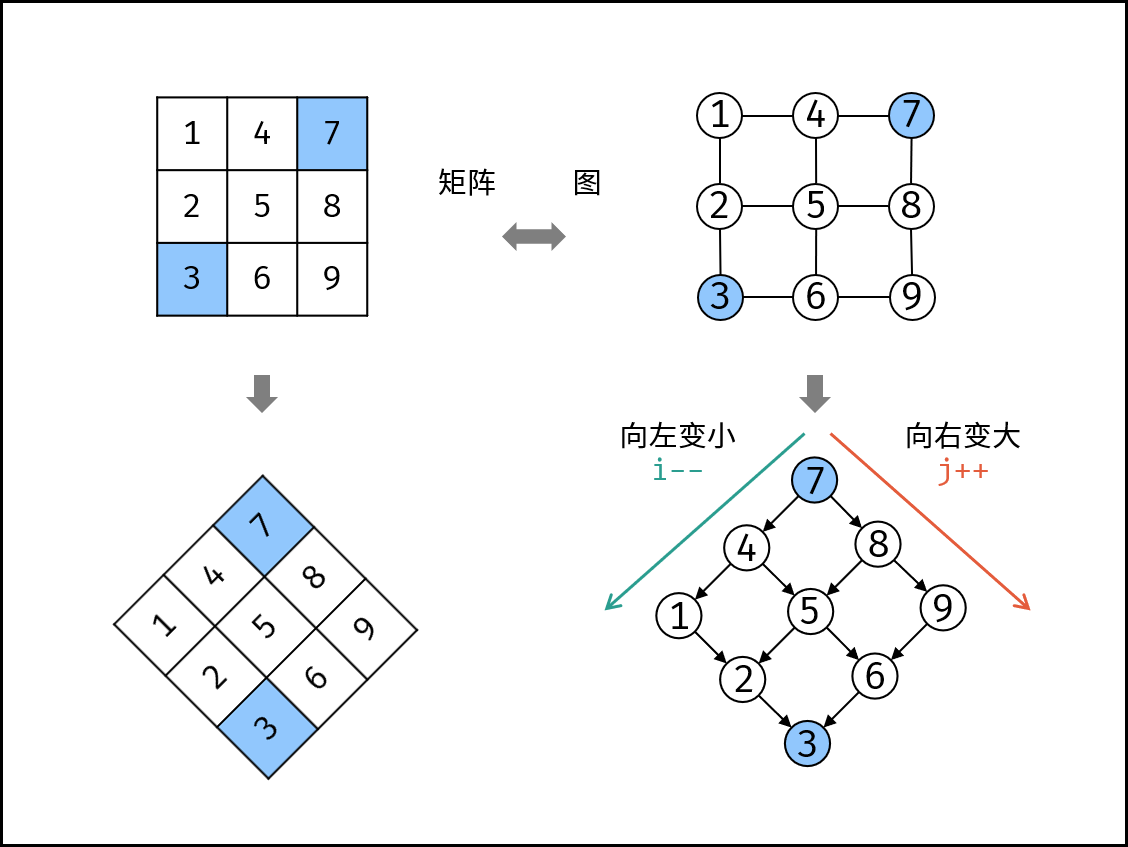
代码展示：

public class Offer {
    public static void main(String[] args) {
        Random random = new Random();
        int target = random.nextInt(100)+1;
        int n = random.nextInt(10)+1;
        int m = random.nextInt(10)+1;
        int[][] arr = new int[n][m];
        int target1,target2;
        for (int i=0;i<n;i++){
            if (i == 0){
                target1 = random.nextInt(10)+1;
            }else {
                target1 = arr[i-1][0]+ random.nextInt(10)+1;
            }
            for (int j=0;j<m;j++){
                if (j == 0){
                    arr[i][j] = target1;
                }else {
                    if (i!=0&&j!=0){
                        target2 = Math.max(arr[i][j-1],arr[i-1][j]);
                    }else {
                        target2 = arr[i][j-1];
                    }
                    arr[i][j] = target2 + random.nextInt(10)+1;
                }
            }
        }
        for (int i=0;i<n;i++){
            System.out.println("参数："+ Arrays.toString(arr[i]));
        }
        System.out.println("参数target："+ target);
        System.out.println(Method2(arr,target));
//        System.out.println(Method2(getArr(),target));
    }

    public static int[][] getArr(){
        int[][] arr = new int[5][5];
        arr[0] = new int[]{1,   4,  7, 11, 15};
        arr[1] = new int[]{2,   5,  8, 12, 19};
        arr[2] = new int[]{3,   6,  9, 16, 22};
        arr[3] = new int[]{10, 13, 14, 17, 24};
        arr[4] = new int[]{18, 21, 23, 26, 30};
        for (int i=0;i<5;i++){
            System.out.println("参数："+ Arrays.toString(arr[i]));
        }
        return arr;
    }

    //思路一:双循环暴力破解，但是这种其实并不可取，但是如果实在想不出，却也是一条路子
    public static boolean Method1(int[][] matrix, int target){
        boolean result = false;
        if (matrix == null) {
            return result;
        }
       for (int[] matrixTemp : matrix){
           for (int temp : matrixTemp){
               if (temp == target){
                   result = true;
               }
           }
       }

        return result;
    }

    //思路二：二分查找,简单点的就是对暴力破解的方法进行优化，因为每一行都是有序的，所以每一行都可以使用二分查找简化时间
    public static boolean Method2(int[][] matrix, int target){
        if (matrix.length == 1 && matrix[0].length == 0){
            return false;
        }
        //对每一行进行遍历
        for (int i = 0; i < matrix.length; i++){
            int left = 0, right = matrix[i].length - 1;
            //进行二分查找
            while (left < right){
                int mid = (right + left)/2;
                if (matrix[i][mid] < target){
                    left = mid + 1;
                }else {
                    right = mid;
                }
            }
            if (matrix[i][left] == target){
                return true;
            }
            //如果当前行没有找到目标且下一行的第一个元素已经大于目标值，则无目标值，数组规模大时可以提高效率
            if (i < matrix.length - 1 && matrix[i + 1][0] > target) {
                return false;
            }
        }
        return false;
    }

    //思路三：二分查找,这种就比较抽象，其实把数据数组向左旋转45度，会发现有点像图的结构
    //而且有规律是的往左走是减，往右走是加。所以按图的方式遍历的话可以省略掉遍历很多数据的功夫
    //0 ms 击败 100%
    //内存 47.3 MB 击败 55.67%
    //这种无疑是最好的，因为遍历少，开辟的额外空间也少
    public static boolean Method3(int[][] matrix, int target){
        int i = matrix.length - 1, j = 0;
        while(i >= 0 && j < matrix[0].length)
        {
            if(matrix[i][j] > target){
                i--;
            }else if(matrix[i][j] < target) {
                j++;
            }else {
                return true;
            }
        }
        return false;
    }
}