容器盛水问题

题目：

 

 

 

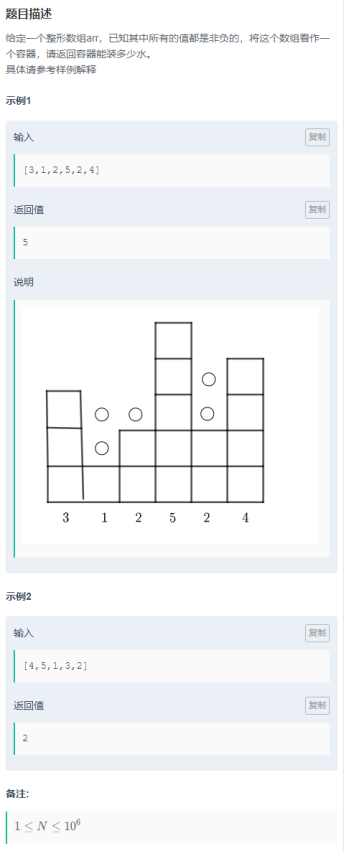
思路：

先是说一说对这道题的理解吧，常规的容器的容量是由最短的边决定的，所以应该取左右两边的最短边减去底高就是容量，所以理想状态是将数组遍历一次，知道每一个低是否有容量，例如L与R是容器的两边，且L比R小，故L决定了容量，设X为容器底，则L-X,会出现两种情况，一是整数，则可以知道容量是多少；二是负数，即这个低比L要高，所以这时候容量应该为0，且这时候L应该变为X即L=X，成为新的容器边，探索下面的低的容量。故我们可以用V=0初始化，然后每次求出容量的时候进行加入，统计出总容量。

这种方法的时间复杂度为O（N），空间复杂度为O(1)。其中需要注意的就是V的取值范围。不然容易会出现溢出问题。

代码示例：

public class Solution {

 

    public static void main(String[] args) {

        int[] arr = {4, 5, 1, 3, 2};

        long result = maxWater(arr);

        System.out.println(result);

    }

 

    /**

     * max water

     *

     * @param arr int整型一维数组 the array

     * @return long长整型

     */

    public static long maxWater(int[] arr) {

        int length = arr.length;

        if (arr == null || length < 3) { //当存在临界值的时候直接返回

            return 0L;

        }

        long value = 0;

        int lmax = arr[0], rmax = arr[length - 1], l = 1, r = length - 2;

        while (l <= r) {

            if (lmax <= rmax) {

                value += Math.max(0, lmax - arr[l]);

                lmax = Math.max(lmax, arr[l++]);

            } else {

                value += Math.max(0, rmax - arr[r]);

                rmax = Math.max(rmax, arr[r--]);

            }

        }

        return value;

    }

}