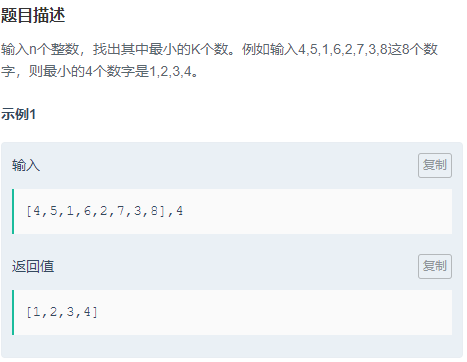
最小的K个数

题目：

 

 

 

思路：

思路一：直接利用快速排序的方法对数组进行排序，时间复杂度为O(NlogN)，简单便捷，排完序之后便是有序的数组，直接去前K个数出来

 

思路二：根据一次快排(Partition)的想法，我们知道一次随机快速排序可以确定一个有序的位置，这个位置的左边都小于这个数，右边都大于这个数，我们如果能找到随机快速排序确定的位置等于k-1的那个位置，那么0-k-1个数就是我们要找的数。怎么能找到那个位置：

如果Partition确定的位置小于K-1，说明k-1这个位置在它的右边，我们继续在右边进行查找。

如果Partition确定的位置大于K-1，说明k-1这个位置在它的左边，我们继续在左边进行查找。

缺点： 这种方法的时间复杂度虽然是O(n)，但是找出来的最小的K个数却不是排序过的。而且这种方法有个限制，就是必须修改给的数组。

 

思路三：利用大顶堆或小顶堆的思路，就是循环一遍数组，先直接将数组的前K个数直接塞入数组TEMP，构建堆。然后从第K个数开始循环，先取出TEMP的第k-1个数值（即最大或者最小），进行比较，如果符合条件（即大于或小于），将堆的K-1踢出，将新值放入，重新构建堆。重复以上步骤直至循环结束。时间复杂度是O(n)，空间复杂度为O(k)

 

代码示例：

import java.util.ArrayList;

import java.util.Collections;

 

public class Solution {

    public static void main(String[] args) {

        int[] input = {4, 5, 1, 6, 2, 7, 3, 8};

        System.out.println(GetLeastNumbers_Solution(input, 0));

    }

 

 

    public static ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {

        ArrayList<Integer> temp = new ArrayList<Integer>();

        if (input.length < k || input.length == 0 || k == 0) {

            return temp;

        }

 

 

        for (int i = 0; i < k; i++) {

            temp.add(input[i]);

        }

        Collections.sort(temp);

        for (int i = k; i < input.length; i++) {

            if (temp.get(k - 1) > input[i]) {

                temp.remove(k - 1);

                temp.add(input[i]);

                Collections.sort(temp);

            }

        }

        return temp;

    }

 

}